垂直于直线x+3y-5=0且经过点P的直线的一般式方程是．题目和参考答案——青夏教育精英家教网—

题目内容

垂直于直线x+3y-5=0且经过点P（-1，0）的直线的一般式方程是

．

考点：直线的一般式方程与直线的垂直关系

专题：直线与圆

分析：由垂直关系可得直线的斜率，可得点斜式方程，化为一般式即可．

解答： 解：∵直线x+3y-5=0的斜率为-

，
∴与其垂直的直线的斜率为3，
∴所求直线的方程为y-0=3（x+1），
化为一般式可得3x-y+3=0
故答案为：3x-y+3=0

点评：本题考查直线的一般式方程和垂直关系，属基础题．

练习册系列答案

相关题目

)，记椭圆的左顶点为A．
（1）求椭圆的方程；
（2）设垂直于y轴的直线l交椭圆于B，C两点，试求△ABC面积的最大值．

设函数f（x）=|x-1|+|x-2|．
①画出函数y=f（x）的图象；
②若不等式|a+b|+|a-b|≥|a|f（x），（a≠0，a、b∈R）恒成立，求实数x的范围．

已知点A（1，-2），B（m，2），且线段AB的垂直平分线的方程是x+2y-2=0，则实数m的值是

．

某实验室某一天的温度（单位：°C）随时间t（单位：h）的变化近似满足函数关系：f（t）=9-

cos

t-sin

t，t∈[0，24）．
（1）求实验室这一天里，温度降低的时间段；
（2）若要求实验室温度不高于10°C，则在哪段时间实验室需要降温？

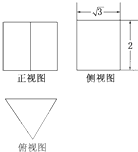如图为一个几何体的三视图，正视图和侧视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的表面积为（　　）

设集合A={x|3x-2＞1}，B={x|2m≤x≤m+3}
①当m=-1时，求A∩B，A∪B；
②若B⊆A，求m的取值范围．

将函数y=sin（x-

）的图象上所有点的横坐标缩短为原来的

（纵坐标不变），再将所得函数的图象向左平移

个单位，则最终所得函数图象对应的解析式为（　　）

试题分类