��Ŀ����
��֪ӳ��f��A��B������B=R����Ӧ����f��x��y=log
��2-x��-
������ʵ��k��B���ڼ���A�в�����ԭ��˵������A��B�������ǿռ��ϣ��������ij�ֶ�Ӧ����f����A������һ��Ԫ��x����B����һ���ҽ���һ��Ԫ��y��x��Ӧ�����f�Ǽ���A������B��ӳ�䣬��ʱ��y��x��ӳ��f�����µ���x����y��ԭ����k��ȡֵ��Χ�ǣ�������
| 1 |
| 2 |
| 1-x |
| A��k��0 | B��k��0 |
| C��k��1 | D�����϶����� |
���㣺ӳ��
ר�⣺�Ķ���,���������ʼ�Ӧ��
������ʵ��k��B���ڼ���A�в�����ԭ��ʾkӦ����A������Ԫ����B�ж�Ӧ����ɵļ��ϵIJ����У������ǿ��Ը�����֪�����е�A��ӳ��f��A��B����Ӧ����Ϊf��x��y=log
��2-x��-
�����A������Ԫ����B�ж�Ӧ������ɵļ��ϣ������䲹�����ɵõ��𰸣�
| 1 |
| 2 |
| 1-x |
���
�⣺����y=log
��2-x��-
���䶨����ΪA={x|2-x��0��1-x��0}={x|x��1}��
����x��1����2-x��1��1-x��0��
��log
��2-x����0��
��0��
��x��Aʱ����ӳ��f��A��B�������¶�Ӧ������㣺y��0����
����ʵ��k��B���ڼ���A�в�����ԭ����kӦ���㣬k��0
������������ʵ��k��ȡֵ��Χ��k��0��
��ѡ��B��
| 1 |
| 2 |
| 1-x |
���䶨����ΪA={x|2-x��0��1-x��0}={x|x��1}��
����x��1����2-x��1��1-x��0��
��log
| 1 |
| 2 |
| 1-x |
��x��Aʱ����ӳ��f��A��B�������¶�Ӧ������㣺y��0����
����ʵ��k��B���ڼ���A�в�����ԭ����kӦ���㣬k��0
������������ʵ��k��ȡֵ��Χ��k��0��
��ѡ��B��
�������ڼ���A��B��ӳ���У�������ʵ��k��B���ڼ���A�в�����ԭ��ʾkӦ����A������Ԫ����B�ж�Ӧ����ɵļ��ϵIJ����У�

��ϰ��ϵ�д�
�����Ŀ
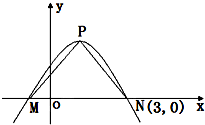 ��P�Ǻ���y=2sin����x+�գ����أ�0����ͼ�����ߵ㣬M��N�����P���ڵ��Ҹ�ͼ����x����������㣬��N��3��0������
��P�Ǻ���y=2sin����x+�գ����أ�0����ͼ�����ߵ㣬M��N�����P���ڵ��Ҹ�ͼ����x����������㣬��N��3��0������| PM |
| PN |
A��
| ||
B��
| ||
| C��4 | ||
| D��8 |
��xΪʵ��������p��?x��R��x2��0��������p�ķ��ǣ�������
| A���Vp��?x0��R��x02��0 |
| B���Vp��?x0��R��x02��0 |
| C���Vp��?x��R��x2��0 |
| D���Vp��?x��R��x2��0 |
��֪��P������y=
�ϣ���Ϊ�����ڵ�P�������ߵ���б�ǣ������ȡֵ��Χ�ǣ�������
| 2 |
| e2x+1 |
A��[0��
| ||||
B��[
| ||||
C����
| ||||
D��[
|
�輯��M={x|1��x��2}��N={x|x��a}����M�ɣ�∁RN��=M����a��ȡֵ��Χ�ǣ�������
| A����-�ޣ�1�� |
| B����-�ޣ�1] |
| C��[1��+�ޣ� |
| D����2��+�ޣ� |
ͬʱ��Ͷ��ö�ʵؾ��ȵ�Ӳ�ң�����öӲ�Ҿ��������ϵĸ���Ϊ��������
A��
| ||
B��
| ||
C��
| ||
| D��1 |