题目内容
在△ABC中,角A,B,C的对边分别是a,b,c.若a=5bsinC,且cosA=5cosBcosC,则tanA的值为( )
| A、5 | B、6 | C、-4 | D、-6 |
考点:正弦定理,两角和与差的余弦函数
专题:三角函数的求值,解三角形
分析:运用正弦定理,把边化成角得到sinA=5sinBsinC,再与条件cosA=5cosBcosC相减,运用两角和的余弦公式,再用诱导公式转化为cosA,由同角公式,即可求出tanA.
解答:
解:∵a=5bsinC,
由正弦定理得:sinA=5sinBsinC①,
又cosA=5cosBcosC②,
②-①得,cosA-sinA=5(cosBcosC-sinBsinC)
=5cos(B+C)=-5cosA,
∴sinA=6cosA,
∴tanA=
=6.
故选B.
由正弦定理得:sinA=5sinBsinC①,
又cosA=5cosBcosC②,
②-①得,cosA-sinA=5(cosBcosC-sinBsinC)
=5cos(B+C)=-5cosA,
∴sinA=6cosA,
∴tanA=
| sinA |
| cosA |
故选B.
点评:本题主要考查解三角形中的正弦定理及应用,同时考查两角和差的余弦公式,诱导公式,以及同角三角函数的关系式,这些都是三角中的基本公式,务必要掌握,注意公式的逆用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且g(x)=f(x-1),则f(2013)+f(2015)的值为( )
| A、-1 | B、1 | C、0 | D、无法计算 |
已知集合A={x|(x-1)(x-5)<0},B={x|0<x≤4},则集合A∩B=( )
| A、{x|0<x<4} |
| B、{x|0<x<5} |
| C、{x|1<x≤4} |
| D、{x|4≤x<5} |
向圆内随机投掷一点,此点落在该圆的内接正n(n≥3,n∈N)边形内的概率为Pn,下列论断正确的是( )
| A、随着n的增大,Pn增大 |
| B、随着n的增大,Pn减小 |
| C、随着n的增大,Pn先增大后减小 |
| D、随着n的增大,Pn先减小后增大 |
已知点P在曲线y=
上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
| 2 |
| e2x+1 |
A、[0,
| ||||
B、[
| ||||
C、(
| ||||
D、[
|
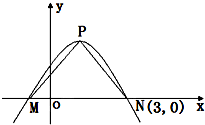 点P是函数y=2sin(ωx+φ)(ω>0)的图象的最高点,M,N是与点P相邻的且该图象与x轴的两个交点,且N(3,0),若
点P是函数y=2sin(ωx+φ)(ω>0)的图象的最高点,M,N是与点P相邻的且该图象与x轴的两个交点,且N(3,0),若