题目内容
在区间[1,5]上任取一个数m,则函数y=x2-4x-2(0≤x≤m)的值域为[-6,-2]的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:找出函数y=x2-4x-2(0≤x≤m)的值域为[-6,-2]时对应的区域长度的大小,再将其与m∈[1,5],表示的长度大小代入几何概型的计算公式进行解答.
解答:
解:当x=2时,y=-6;当x=0或4时,y=-2.
即m∈[2,4]时,函数y=x2-4x-2(0≤x≤m)值域为[-6,-2],
则所求概率为P=
=
,
故选:C.
即m∈[2,4]时,函数y=x2-4x-2(0≤x≤m)值域为[-6,-2],
则所求概率为P=
| 4-2 |
| 5-1 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查了几何概型、二次函数的性质.几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果函数y=|cos(
+ax)|的图象关于直线x=π对称,则正实数a的最小值是( )
| π |
| 4 |
A、a=
| ||
B、a=
| ||
C、a=
| ||
| D、a=1 |
已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且g(x)=f(x-1),则f(2013)+f(2015)的值为( )
| A、-1 | B、1 | C、0 | D、无法计算 |
已知不等式
+
>
对任意正数x、y恒成立,则实数k的取值范围是( )
| 1 |
| x |
| 9 |
| y |
| k |
| x+y |
| A、k<16 | B、k>16 |
| C、k>12 | D、k<12 |
设x为实数,命题p:?x∈R,x2≥0,则命题p的否定是( )
| A、¬p:?x0∈R,x02<0 |
| B、¬p:?x0∈R,x02≤0 |
| C、¬p:?x∈R,x2<0 |
| D、¬p:?x∈R,x2≤0 |
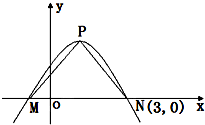 点P是函数y=2sin(ωx+φ)(ω>0)的图象的最高点,M,N是与点P相邻的且该图象与x轴的两个交点,且N(3,0),若
点P是函数y=2sin(ωx+φ)(ω>0)的图象的最高点,M,N是与点P相邻的且该图象与x轴的两个交点,且N(3,0),若