题目内容
已知sin2(α+γ)=nsin2β,则
=( )
| tan(α+β+γ) |
| tan(α-β+γ) |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:依题意知,sin[(α+β+γ )+(α-β+γ)]=nsin[(α+β+γ)-(α-β+γ)],展开整理即可.
解答:
解:∵sin2(α+γ)=nsin2β,
即:sin[(α+β+γ )+(α-β+γ)]=nsin[(α+β+γ)-(α-β+γ)],
∴sin(α+β+γ)•cos(α-β+γ)+cos(α+β+γ)•sin(α-β+γ)=n[sin(α+β+γ)•cos(α-β+γ)-cos(α+β+γ)•sin(α-β+γ),
∴(1-n)sin(α+β+γ)•cos(α-β+γ)=(-1-n)cos(α+β+γ)•sin(α-β+γ),
∴tan(α+β+γ)•cot(α-β+γ)=
,
即
=
,
故选:D.
即:sin[(α+β+γ )+(α-β+γ)]=nsin[(α+β+γ)-(α-β+γ)],
∴sin(α+β+γ)•cos(α-β+γ)+cos(α+β+γ)•sin(α-β+γ)=n[sin(α+β+γ)•cos(α-β+γ)-cos(α+β+γ)•sin(α-β+γ),
∴(1-n)sin(α+β+γ)•cos(α-β+γ)=(-1-n)cos(α+β+γ)•sin(α-β+γ),
∴tan(α+β+γ)•cot(α-β+γ)=
| n+1 |
| n-1 |
即
| tan(α+β+γ) |
| tan(α-β+γ) |
| n+1 |
| n-1 |
故选:D.
点评:本题考查同角三角函数基本关系的运用,考查观察与拆、凑角的能力,考查转化思想与运算能力,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
如果函数y=|cos(
+ax)|的图象关于直线x=π对称,则正实数a的最小值是( )
| π |
| 4 |
A、a=
| ||
B、a=
| ||
C、a=
| ||
| D、a=1 |
已知不等式
+
>
对任意正数x、y恒成立,则实数k的取值范围是( )
| 1 |
| x |
| 9 |
| y |
| k |
| x+y |
| A、k<16 | B、k>16 |
| C、k>12 | D、k<12 |
已知函数f(x)=sin(ωx+φ),对任意的实数x均存在a使得f(a)≤f(x)≤f(0)成立,且|a|的最小值为
,则函数f(x)的单调递减区间为( )
| π |
| 2 |
A、[kπ-
| ||
B、[kπ,kπ+
| ||
C、[2kπ-
| ||
D、[2kπ,2kπ+
|
设x为实数,命题p:?x∈R,x2≥0,则命题p的否定是( )
| A、¬p:?x0∈R,x02<0 |
| B、¬p:?x0∈R,x02≤0 |
| C、¬p:?x∈R,x2<0 |
| D、¬p:?x∈R,x2≤0 |
设集合M={x|1<x≤2},N={x|x≤a},若M∩(∁RN)=M,则a的取值范围是( )
| A、(-∞,1) |
| B、(-∞,1] |
| C、[1,+∞) |
| D、(2,+∞) |
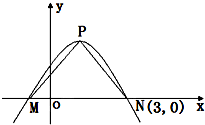 点P是函数y=2sin(ωx+φ)(ω>0)的图象的最高点,M,N是与点P相邻的且该图象与x轴的两个交点,且N(3,0),若
点P是函数y=2sin(ωx+φ)(ω>0)的图象的最高点,M,N是与点P相邻的且该图象与x轴的两个交点,且N(3,0),若