题目内容
已知函数f(x)=ax3+bx2+cx+d(a≠0),证明:f(x)是中心对称图形.
考点:导数的运算,函数奇偶性的判断
专题:函数的性质及应用
分析:将已知的函数求导,利用导数的几何意义证明.
解答:
证明:∵f(x)=ax3+bx2+cx+d(a≠0),
∴f′(x)=3ax2+2bx+c,f″(x)=6ax+2b,
∵f″(x)=6a×(-
)+2b=0,
∴任意三次函数都关于点(-
,f(-
))对称,
所以f(x)是中心对称图形.
∴f′(x)=3ax2+2bx+c,f″(x)=6ax+2b,
∵f″(x)=6a×(-
| b |
| 3a |
∴任意三次函数都关于点(-
| b |
| 3a |
| b |
| 3a |
所以f(x)是中心对称图形.
点评:本题考查了3次函数都是中心对称图形,关键是结合导数的几何意义解答.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
复数
化简是( )
| 1-i |
| i |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
根据工作需要,现从4名女医生,a名男医生中选3名医生组成一个救援团队,其中a=
xdx,则团队中男、女医生都有的概率为( )
| ∫ | 1 0 |
| 5 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
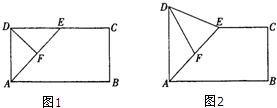 如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.
如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.