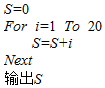题目内容
15.已知集合M={1,2,3,…,n,n+1}(n≥2,n∈N),M1,M2,M3,…,MS(k)是M的k+1元子集(k∈N,k≤n)(1)若n=9,k=1,且满足Mi(i∈{1,2,…,S(k)}中各元素之和是3的倍数,求S(k)的值;
(2)若满足M(i∈{1,2,…,S(k)}中必含有元素3,
①求S(k)的表达式;
②设bk=(-1)k+1$\frac{k+1}{n-k}$S(k+1),Tm=b0+b1+b2+…+bm(m∈N*,m≤n-1),求|$\frac{{T}_{m}}{{C}_{n-1}^{m}}$|的值.
分析 (1)直接利用列举法写出集合M的所有2元子集求得S(k)的值;
(2)①S(k)是从除3外的n个元素中任取k个元素的组合数;
②由组合数的阶乘公式可得bk=(-1)k+1•${C}_{n}^{k}$,再由组合数的性质,可得当1≤k≤n-1时,bk=(-1)k+1•${C}_{n}^{k}$=(-1)k+1•(${C}_{n-1}^{k}+{C}_{n-1}^{k-1}$)
=(-1)k+1•${C}_{n-1}^{k}$+(-1)k+1•${C}_{n-1}^{k-1}$=(-1)k-1•${C}_{n-1}^{k-1}$-(-1)k•${C}_{n-1}^{k}$,讨论m=0和1≤m≤n-1时,计算化简即可得到所求值.
解答 解:(1)n=9,k=1时,M={1,2,3,…,10},
满足条件的2元子集为{1,2},{1,5},{1,8},{2,4},{2,8},{2,10},{3,6},{3,9},{4,5},{4,8},{5,7},{5,10},{6,9},{7,8},{8,10}共15个,故S(k)=15;
(2)①Mi(i∈{1,2,…,S(k)}中比含有元素3,
当k=0时,S(k)=1;
当k=1时,S(k)=n;
当k=2时,S(k)=${C}_{n}^{2}$;
…
当k=n时,S(k)=${C}_{n}^{n}$.
∴S(k)=${C}_{n}^{k}$;
②bk=(-1)k+1$\frac{k+1}{n-k}$S(k+1)=$(-1)^{k+1}\frac{k+1}{n-k}•{C}_{n}^{k+1}$
=$(-1)^{k+1}\frac{k+1}{n-k}•\frac{n!}{(k+1)!•(n-k-1)!}$=$(-1)^{k+1}\frac{n!}{k!(n-k)!}$=$(-1)^{k+1}{C}_{n}^{k}$,
∴当1≤k≤n-1时,bk=(-1)k+1•${C}_{n}^{k}$=(-1)k+1•(${C}_{n-1}^{k}+{C}_{n-1}^{k-1}$)
=(-1)k+1•${C}_{n-1}^{k}$+(-1)k+1•${C}_{n-1}^{k-1}$=(-1)k-1•${C}_{n-1}^{k-1}$-(-1)k•${C}_{n-1}^{k}$,
当m=0时,|$\frac{{T}_{m}}{{C}_{n-1}^{m}}$|=|$\frac{{b}_{0}}{{C}_{n-1}^{0}}$|=1;
当1≤m≤n-1时,Tm=b0+b1+b2+…+bm=-1+$\sum_{k=1}^{m}$[(-1)k-1•${C}_{n-1}^{k-1}$-(-1)k•${C}_{n-1}^{k}$]
=-1+1-(-1)m ${C}_{n-1}^{m}$=-(-1)m ${C}_{n-1}^{m}$,
即有|$\frac{{T}_{m}}{{C}_{n-1}^{m}}$|═1.
综上可得,|$\frac{{T}_{m}}{{C}_{n-1}^{m}}$|=1.
点评 本题考查数列求和,考查了二项式定理和性质的运用,考查组合数公式和性质的运用,训练了运算能力,属于中档题.

| A. | y=cos2x | B. | y=-cos2x | C. | y=sin(2x-$\frac{π}{4}$) | D. | y=-sin2x |
| A. | a<1 | B. | a≤1 | C. | a≥0 | D. | a≤0 |
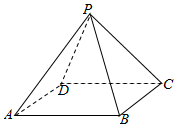 如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.
如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.