题目内容

如果(4x2-
2
x3
)n的展开式中含有非零常数项，则正整数n的最小值为（　　）
A、3B、5C、6D、10
考点：二项式系数的性质
专题：二项式定理
分析：可得展开式的通项为Tk+1=
C
k
n
4n-k（-2）kx2n-5k，令2n-5k=0易得答案．
解答： 解：(4x2-
2
x3
)n的展开式的通项为Tk+1=
C
k
n
（4x2）n-k（-2x-3）k
=
C
k
n
4n-k（-2）kx2n-5k，令2n-5k=0可得n=
5k
2
，
∴当k=2时，正整数n取最小值5
故选：B
点评：本题考查二项式定理，属基础题．
练习册系列答案
相关题目
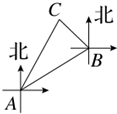如图，某海上缉私小分队驾驶缉私艇以40km/h的速度由A处出发，沿北偏东60°方向进行海面巡逻，当航行半小时到达B处时，发现北偏西45°方向有一艘船C，若船C位于A的北偏东30°方向上，则缉私艇所在的B处与船C的距离是（　　）km．
A、5（
6
+
2
）
B、5（
6
-
2
）
C、10（
6
-
2
）
D、10（
6
+
2
）
已知
AB
=（1，3），
BC
=（2，-1），
OC
=-
1
3
AC
，则C点的坐标为
 
．
满足A∪{-1，1}={-1，0，1}的集合A共有（　　）
A、10个B、8个C、6个D、4个
α，β是两个不重合的平面，在下列条件中，可判定α∥β的是（　　）
A、α，β都与平面γ垂直
B、α内不共线的三点到β的距离相等
C、l，m是α内的两条直线且l∥β，m∥β
D、l，m是两条异面直线且l∥α，m∥α，l∥β，m∥β
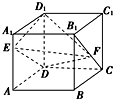如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为线段AA1，B1C上的点，则三棱锥D1-EDF的体积为（　　）
A、
1
8
B、
1
6
C、
1
3
D、
1
2
已知二次函数f（x）=ax2+bx+c（其中a≠0）满足下列3个条件：
①f（x）的图象过坐标原点；
②对于任意x∈R都有f(-
1
2
+x)=f(-
1
2
-x)成立；
③方程f（x）=x有两个相等的实数根，令g（x）=f（x）-|λx-1|（其中λ＞0），
（1）求函数f（x）的表达式；
（2）求函数g（x）的单调区间（直接写出结果即可）；
（3）研究函数g（x）在区间（0，1）上的零点个数．
已知抛物线y2=2px过点M（
1
4
，
2
2
），A，B是抛物线上的点，直线OA，OM，OB的斜率成等比数列，则直线AB恒过定点
 
．
给出以下四个命题：
①若A＞B，则cosA＜cosB；
②“若a+b≥2，则a，b 中至少有一个不小于1”的逆命题；
③“若x2+y2=0，则x，y都为0”的否命题；
④若x+y≠3，则x≠1或y≠2．
其中真命题是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网