题目内容
3.已知点P的坐标(x,y)满足$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$过点P的直线l与圆O:x2+y2=7交于A,B两点,则|AB|的最小值为( )| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
分析 由约束条件作出可行域,求出可行域内到原点距离最远的点,然后结合弦心距、圆的半径及弦长间的关系得答案.
解答 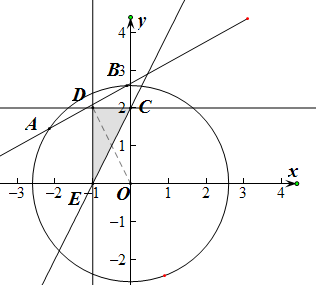 解:不等式可行域$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$如图所示
解:不等式可行域$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$如图所示
联立$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,解得D(-1,2).
由图可知,可行域内的点中,
D 到原点的距离最大为$\sqrt{5}$,
∴|AB|的最小值为2$\sqrt{7-5}$=2$\sqrt{2}$.
故选B
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,训练了直线与圆位置关系的应用,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.复数$z=\frac{-1+i}{2-i}$的虚部为( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $-\frac{1}{5}$ |

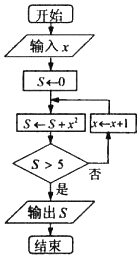 据记载,在公元前3世纪,阿基米德已经得出了前n个自然数平方和的一般公式.如图是一个求前n个自然数平方和的算法流程图,若输入x的值为1,则输出的S的值为14.
据记载,在公元前3世纪,阿基米德已经得出了前n个自然数平方和的一般公式.如图是一个求前n个自然数平方和的算法流程图,若输入x的值为1,则输出的S的值为14.