题目内容
已知α,β∈(
,π),sin(α+β)=-
,cos(β-
)=-
,则cos(α+
)= .
| 3π |
| 4 |
| 4 |
| 5 |
| π |
| 4 |
| 12 |
| 13 |
| π |
| 4 |
考点:两角和与差的余弦函数,两角和与差的正弦函数
专题:三角函数的求值
分析:利用同角三角函数间的关系式可求得cos(α+β)与sin(β-
)的值,再利用两角差的余弦可求得cos(α+
)=cos[(α+β)-(β-
)]的值.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:
解:∵α,β∈(
,π),
∴α+β∈(
,2π),β-
∈(
,
),
又sin(α+β)=-
,cos(β-
)=-
,
∴cos(α+β)=
=
,sin(β-
)=
=
,
∴cos(α+
)=cos[(α+β)-(β-
)]
=cos(α+β)cos(β-
)+sin(α+β)sin(β-
)
=
×(-
)+(-
)×
=-
.
故答案为:-
.
| 3π |
| 4 |
∴α+β∈(
| 3π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
又sin(α+β)=-
| 4 |
| 5 |
| π |
| 4 |
| 12 |
| 13 |
∴cos(α+β)=
| 1-sin2(α+β) |
| 3 |
| 5 |
| π |
| 4 |
1-cos2(β-
|
| 5 |
| 13 |
∴cos(α+
| π |
| 4 |
| π |
| 4 |
=cos(α+β)cos(β-
| π |
| 4 |
| π |
| 4 |
=
| 3 |
| 5 |
| 12 |
| 13 |
| 4 |
| 5 |
| 5 |
| 13 |
| 56 |
| 65 |
故答案为:-
| 56 |
| 65 |
点评:本题考查同角三角函数间的关系式与两角差的余弦,考查化归思想与运算求解能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 运行如图所示的程序框图,输出A,B,C的一组数据为
运行如图所示的程序框图,输出A,B,C的一组数据为 | 3 |
| A、垂直、相切 |
| B、平行、相交 |
| C、垂直、相离 |
| D、平行、相切 |
若ax(1+
)5的展开式中x2项的系数是20,则实数a等于( )
| x |
| A、2 | B、3 | C、4 | D、5 |
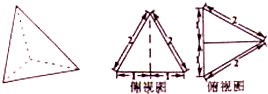 某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是
某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是 用4种不同的颜色给图中A、B、C、D四个区域涂色,要求相邻的区域涂色不同,则不同的涂色方法共有
用4种不同的颜色给图中A、B、C、D四个区域涂色,要求相邻的区域涂色不同,则不同的涂色方法共有