题目内容
下列命题正确的有 (填序号)
(1)经过三点确定一个平面;
(2)若a∥b且a⊥c,则b⊥c;
(3)若a⊥c且b⊥c,则a∥b;
(4)没有公共点的两条直线是异面直线;
(5)两两相交且不共点的三条直线确定一个平面.
(1)经过三点确定一个平面;
(2)若a∥b且a⊥c,则b⊥c;
(3)若a⊥c且b⊥c,则a∥b;
(4)没有公共点的两条直线是异面直线;
(5)两两相交且不共点的三条直线确定一个平面.
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据空间直线的位置分别进行判断即可得到结论.
解答:
解:(1)经过不公线的三点确定一个平面,当三点共线时,有很多平面.;
(2)根据直线平行的性质可知,若a∥b且a⊥c,则b⊥c成立;
(3)垂直于同一直线的两条直线不一定平行,故若a⊥c且b⊥c,则a∥b不一定成立;
(4)当直线平行时,两条直线没有公共点,但此时两条直线不是异面直线;
(5)两两相交且不共点的三条直线确定一个平面.正确.
故正确是(2)(5),
故答案为:(2)(5)
(2)根据直线平行的性质可知,若a∥b且a⊥c,则b⊥c成立;
(3)垂直于同一直线的两条直线不一定平行,故若a⊥c且b⊥c,则a∥b不一定成立;
(4)当直线平行时,两条直线没有公共点,但此时两条直线不是异面直线;
(5)两两相交且不共点的三条直线确定一个平面.正确.
故正确是(2)(5),
故答案为:(2)(5)
点评:本题主要考查空间直线和平面位置关系的判断,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
相关题目
函数y=sinx-
cosx的一个单调区间是( )
| 3 |
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
三棱锥A-BCD中,三条侧棱两两互相垂直,AB=3,AC=4,AD=12,则三棱锥A-BCD的外接球的表面积为( )
| A、153π | B、160π |
| C、169π | D、360π |
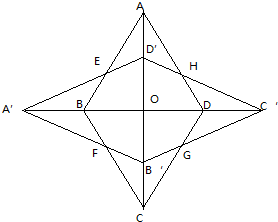 如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.
如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.