Question

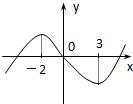函数f（x）=x³+bx²+cx+d，图象如图，则函数y=log2(x2+

2

3

bx+

c

3

)的单调递减区间为（　　）

• A、[

  1

  2

  ，+∞）
• B、[3，+∞）
• C、[-2，3]
• D、（-∞，-2）

Answer 1

考点：利用导数研究函数的单调性,复合函数的单调性

专题：导数的综合应用

分析：求出原函数的导函数，由图象得到f′（-2）=f（3）=0，联立求得b，c的值，代入g（x）=x2+

2

3

bx+

c

3

，由g（x）＞0求得x的范围，再由导数求出函数g（x）的减区间，则函数y=log2(x2+

2

3

bx+

c

3

)的单调递减区间可求．

解答： 解：∵f（x）=x³+bx²+cx+d，
∴f′（x）=3x²+2bx+c，
由图可知f′（-2）=f（3）=0．
∴

12-4b+c=0 27+6b+c=0

，解得

b=- 3 2 c=-18

．
令g（x）=x2+

2

3

bx+

c

3

，
则g（x）=x²-x-6，g′（x）=2x-1．
由g（x）=x²-x-6＞0，解得x＜-2或x＞3．
当x＜

1

2

时，g′（x）＜0，
∴g（x）=x²-x-6在（-∞，-2）上为减函数．
∴函数y=log2(x2+

2

3

bx+

c

3

)的单调递减区间为（-∞，-2）．
故选：D．

点评：本题考查了利用导数研究函数的单调性，训练了简单的复合函数单调性的求法，关键是注意函数的定义域，是中档题．