题目内容
已知f(n+1)=
,f(1)=1(n∈N*),猜想f(n)的表达式为( )
| 3f(n) |
| f(n)+3 |
A、f(n)=
| ||
B、f(n)=
| ||
C、f(n)=
| ||
D、f(n)=
|
考点:归纳推理
专题:规律型
分析:根据题意,f(1)=1,f(n+1)=
,依次求出f(2)、f(3)、f(4)…,进而可以发现规律,得到答案.
| 3f(n) |
| f(n)+3 |
解答:
解:根据题意,f(1)=1,f(n+1)=
,
f(2)=
=
,
f(3)=
=
,
f(4)=
=
=
…
可以归纳f(x)为分数,且其分子为3不变,分母为n+2;
即f(n)=
,
故选:A
| 3f(n) |
| f(n)+3 |
f(2)=
| 3×1 |
| 1+3 |
| 3 |
| 4 |
f(3)=
3×
| ||
|
| 3 |
| 5 |
f(4)=
3×
| ||
|
| 1 |
| 2 |
| 3 |
| 6 |
…
可以归纳f(x)为分数,且其分子为3不变,分母为n+2;
即f(n)=
| 3 |
| n+2 |
故选:A
点评:本题考查归纳推理,关键在求出f(2)、f(3)、f(4)值后,分析其值的变化规律,得到答案.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
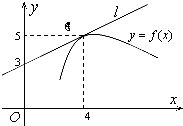
如图,直线l是曲线y=f(x)在x=4处的切线,则f′(4)=( )

A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
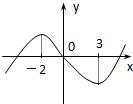 函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+
函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+| 2 |
| 3 |
| c |
| 3 |
A、[
| ||
| B、[3,+∞) | ||
| C、[-2,3] | ||
| D、(-∞,-2) |
设某种植物由出生算起长到1m的概率为0.8,长到2m的概率为0.4,现有一个1m的这种植物,它能长到2m的概率是( )
| A、0.32 | B、0.4 |
| C、0.5 | D、0.8 |
如图程序执行后输出的结果是( )


| A、1 | B、2 | C、3 | D、4 |
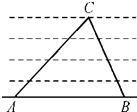 如图,为了测定河的宽度,在一岸边选定两点A,B和对岸标记物C,测得∠CAB=30°,∠CBA=45°,AB=120m,则河的宽度为
如图,为了测定河的宽度,在一岸边选定两点A,B和对岸标记物C,测得∠CAB=30°,∠CBA=45°,AB=120m,则河的宽度为