题目内容
等比数列{an}中，a2a4=16，则a1a5=（ ）
| A、4 | B、16 | C、-4 | D、-16 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：由等比数列的性质可得a2a4=a12q4，也可得a1a5=a12q4，代换即可．
解答：
解：设等比数列{an}的公比为q，
则a2a4=a1q•a1q3=a12q4=16
∴a1a5=a1•a1q4=a12q4=16
故选：B
则a2a4=a1q•a1q3=a12q4=16
∴a1a5=a1•a1q4=a12q4=16
故选：B
点评：本题考查等比数列的性质，属基础题．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
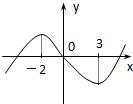函数f（x）=x3+bx2+cx+d，图象如图，则函数y=log2(x2+| 2 |
| 3 |
| c |
| 3 |
A、[
| ||
| B、[3，+∞） | ||
| C、[-2，3] | ||
| D、（-∞，-2） |
下列式子中，表示残差平方和的是（ ）
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
如图程序执行后输出的结果是（ ）
| A、1 | B、2 | C、3 | D、4 |
直线l：y+kx+2=0与曲线C：ρ=2cosθ有交点，则k的取值范围是（ ）
A、k≤-
| ||
B、k≥-
| ||
| C、k∈R | ||
| D、k∈R但k≠0 |
已知复数z=（x2-2x-3）+（x-3）i（x∈R，i为虚数单位）为纯虚数，则x的值为（ ）
| A、-1或3 | B、0 | C、3 | D、-1 |
观察下列各式：已知a+b=1，a2+b2=3，a3+b3=4，a4+b4=7，a5+b5=11，…，则归纳猜测a7+b7=（ ）
| A、26 | B、27 | C、28 | D、29 |
在三角形△ABC所在的平面上有一点P，满足6
=3
+2
，则△PBC与△ABC的面积之比是（ ）
| AP |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|