题目内容
在内接于半径为R的半圆的矩形中,周长最大的矩形的边长为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、以上都不对 |
考点:基本不等式
专题:不等式的解法及应用
分析:如图所示:矩形的长为2Rcosθ,宽为 Rsinθ,故矩形的周长为4Rcosθ+2Rsinθ=2
R sin(θ+∅),矩形的周长的最大时有
cosθ+
sinθ=1,解出cosθ 和sinθ 的值,即可求得所求.
| 5 |
| 2 | ||
|
| 1 | ||
|
解答:
 解:如图所示:设矩形ABCD,∠AOB=θ,
解:如图所示:设矩形ABCD,∠AOB=θ,
由题意可得矩形的长为2Rcosθ,宽为 Rsinθ,
故矩形的周长为4Rcosθ+2Rsinθ=2
R (
cosθ+
sinθ)=2
Rsin(θ+∅),
其中,sin∅=
,cos∅=
.故矩形的周长的最大值等于2
R,此时,sin(θ+∅)=1.
即
cosθ+
sinθ=1,再由sin2θ+cos2θ=1可得cosθ=
,sinθ=
,
故矩形的长为 2R
=
R,宽为
R,
故选:B.
 解:如图所示:设矩形ABCD,∠AOB=θ,
解:如图所示:设矩形ABCD,∠AOB=θ,由题意可得矩形的长为2Rcosθ,宽为 Rsinθ,
故矩形的周长为4Rcosθ+2Rsinθ=2
| 5 |
| 2 | ||
|
| 1 | ||
|
| 5 |
其中,sin∅=
| 2 | ||
|
| 1 | ||
|
| 5 |
即
| 2 | ||
|
| 1 | ||
|
| 2 | ||
|
| 1 | ||
|
故矩形的长为 2R
| 2 | ||
|
4
| ||
| 5 |
| ||
| 5 |
故选:B.
点评:本题考查两角和的正弦公式,同角三角函数的基本关系,正弦函数的值域,得到
cosθ+
sinθ=1,是解题的关键.
| 2 | ||
|
| 1 | ||
|

练习册系列答案
相关题目
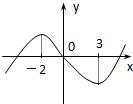 函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+
函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+| 2 |
| 3 |
| c |
| 3 |
A、[
| ||
| B、[3,+∞) | ||
| C、[-2,3] | ||
| D、(-∞,-2) |
设函数f(x)在R 上有定义,给出下列函数:
(1)y=-|f(x)|;
(2)y=f(|x|);
(3)y=-f(-x);
(4)y=f(x)-f(-x);
其中为奇函数的有( )
(1)y=-|f(x)|;
(2)y=f(|x|);
(3)y=-f(-x);
(4)y=f(x)-f(-x);
其中为奇函数的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
设某种植物由出生算起长到1m的概率为0.8,长到2m的概率为0.4,现有一个1m的这种植物,它能长到2m的概率是( )
| A、0.32 | B、0.4 |
| C、0.5 | D、0.8 |
已知角α的终边经过点P(3t,-4t)(t≠0),则sinα+cosα的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、±
|
下列式子中,表示残差平方和的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
观察下列各式:已知a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则归纳猜测a7+b7=( )
| A、26 | B、27 | C、28 | D、29 |

