题目内容
已知函数f(x)=ex+x-m在(1,2)内有零点,g(x)=ln(x-m)在(4,6)内有零点,若m为整数,则m的值为 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据函数零点的存在条件,建立条件关系即可得到结论.
解答:
解:∵f(x)=ex+x-m在(1,2)上单调递增,g(x)=ln(x-m)在(4,6)单调递增,
∴若f(x)=ex+x-m在(1,2)内有零点,则f(1)f(2)<0,
即(e+1-m)(e2+2-m)<0,解得e+1<m<e2+2;
若g(x)=ln(x-m)在(4,6)内有零点,
由g(x)=ln(x-m)=0得x-m=1,
即x=m+1,
由4<m+1<6,解得3<m<5,
综上
,
则e+1<m<5,
若m为整数,则m的值等于4,
故答案为:4
∴若f(x)=ex+x-m在(1,2)内有零点,则f(1)f(2)<0,
即(e+1-m)(e2+2-m)<0,解得e+1<m<e2+2;
若g(x)=ln(x-m)在(4,6)内有零点,
由g(x)=ln(x-m)=0得x-m=1,
即x=m+1,
由4<m+1<6,解得3<m<5,
综上
|
则e+1<m<5,
若m为整数,则m的值等于4,
故答案为:4
点评:本题主要考查函数零点的应用,考查学生的计算能力.要求熟练掌握函数零点的判定条件.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
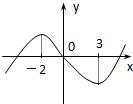 函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+
函数f(x)=x3+bx2+cx+d,图象如图,则函数y=log2(x2+| 2 |
| 3 |
| c |
| 3 |
A、[
| ||
| B、[3,+∞) | ||
| C、[-2,3] | ||
| D、(-∞,-2) |
下列式子中,表示残差平方和的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|

