题目内容
已知函数f(x)=3ln(x+1)+ax2-2x,a∈R,若f(x)在区间(0,+∞)单调递增,求a的范围.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求导函数,利用函数f(x)=3ln(x+1)+ax2-2x,在(0,+∞)上为单调递增函数,构建不等式,即可求实数a的取值范围.
解答:
解:求导函数可得f′(x)=
+2ax-2,
∵函数f(x)=3ln(x+1)+ax2-2x,在(0,+∞)上为单调递增函数,
∴f′(x)=
+2ax-2≥0,即a≥
在(0,+∞)上恒成立,
∵
=
=
=
,
∴当x∈(0,
)时,令g(x)=
,g′(x)=
=
>0,
∴g(x)在(0,
)上是增函数,∴g(x)<g(
)=0,
∴a≥0
当x∈(
,+∞)时,
≤
=2-
,x=
时等号成立.
∴a≥2-
;
∴综上所述a的范围是[0,+∞).
| 3 |
| x+1 |
∵函数f(x)=3ln(x+1)+ax2-2x,在(0,+∞)上为单调递增函数,
∴f′(x)=
| 3 |
| x+1 |
| 2x-1 |
| 2x(x+1) |
∵
| 2x-1 |
| 2x(x+1) |
x-
| ||
| x2+x |
x-
| ||||||
(x-
|
| 1 | ||||||||
(x-
|
∴当x∈(0,
| 1 |
| 2 |
| 2x-1 |
| 2x(x+1) |
-x2+x+
| ||
| (x2+x)2 |
-(x-
| ||||
| (x2+x)2 |
∴g(x)在(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴a≥0
当x∈(
| 1 |
| 2 |
| 1 | ||||||||
(x-
|
| 1 | ||||
2
|
| 3 |
1+
| ||
| 2 |
∴a≥2-
| 3 |
∴综上所述a的范围是[0,+∞).
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查学生的计算能力,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知集合M={x|y=lg
},N={y|y=x2+2x+3},则(∁RM)∩N=( )
| 1-x |
| x |
| A、{x|10<x<1} |
| B、{x|x>1} |
| C、{x|x≥2} |
| D、{x|1<x<2} |
若α是三角形的一个内角,且sinα+cosα=
,则三角形的形状为( )
| 1 |
| 5 |
| A、钝角三角形 | B、锐角三角形 |
| C、直角三角形 | D、无法确定 |
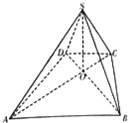 如图所示,四棱锥S-ABCD的底面ABCD为等腰梯形,AB∥CD,对角线AC与BD交于点O,OA=3,OD=1,CD=
如图所示,四棱锥S-ABCD的底面ABCD为等腰梯形,AB∥CD,对角线AC与BD交于点O,OA=3,OD=1,CD=