题目内容
5.设f(x)=$\frac{-{2}^{x}+m}{{2}^{x+1}+n}$(m>0,n>0).(1)当m=n=1时,证明:f(x)不是奇函数;
(2)设f(x)是奇函数,求m与n的值;
(3)在(2)的条件下,求不等式f(f(x))+f($\frac{3}{10}$)<0的解集.
分析 (1)通过当m=n=1时,化简f(x),通过求解f(-1)≠-f(1),证明f(x)不是奇函数.
(2)通过f(-x)=-f(x),通过待定系数法求解即可.
(3)判断f(x)是R上单调减函数.利用单调性转化求解不等式即可.
解答 (1)证明:当m=n=1时,f(x)=$\frac{-{2}^{x}+1}{{2}^{x+1}+1}$.
由于f(1)=$\frac{-2+1}{{2}^{2}+1}$=-$\frac{1}{5}$,f(-1)=$\frac{-\frac{1}{2}+1}{1+1}$=$\frac{1}{4}$,
所以f(-1)≠-f(1),f(x)不是奇函数.
(2)解:f(x)是奇函数时,f(-x)=-f(x),
即$\frac{-{2}^{-x}+m}{{2}^{-x+1}+n}$=-$\frac{-{2}^{x}+m}{{2}^{x+1}+n}$,对定义域内任意实数x成立.
化简整理得(2m-n)•22x+(2mn-4)•2x+(2m-n)=0,这是关于x的恒等式,
所以2mn-4=0,2m-n=0解得n=-2或n=2.
经检验m=1,n=2符合题意.
(3)解:由(2)可知,f(x)=$\frac{-{2}^{x}+1}{{2}^{x+1}+2}$,
易判断f(x)是R上单调减函数.
由f(f(x))+f($\frac{3}{10}$)<0,得
f(f(x))<f($\frac{3}{10}$),f(x)>-$\frac{3}{10}$,2x<4,得x<2
即f(x)>0的解集为(-∞,2).
点评 本题考查函数与方程的综合应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
16.设U=R,A={x|log2x>1},B={x|2x>1},则B∩∁UA=( )
| A. | {x|x>0} | B. | {x|x>2} | C. | {x|0<x≤2} | D. | {x|0≤x<1} |
13.某四棱锥的三视图如图所示,则该四棱锥的外接球的表面积是( )
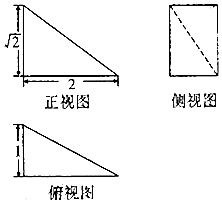

| A. | 4π | B. | 6π | C. | 7π | D. | 12π |
17.已知两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,则下列结论不正确的是( )
| A. | $\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为cosθ | B. | $\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$ | ||
| C. | ($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$) | D. | |$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=1 |
14.与椭圆$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1有公共焦点,且离心率e=$\frac{5}{3}$的双曲线方程是( )
| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1 |
15.若函数f(x)=ax-lnx在x=$\frac{\sqrt{2}}{2}$处取得极值,则实数a的值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |