题目内容
15.若函数f(x)=ax-lnx在x=$\frac{\sqrt{2}}{2}$处取得极值,则实数a的值为( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
分析 先求函数的定义域,然后求出导函数,根据f(x)在x=$\frac{\sqrt{2}}{2}$处取得极值,则f′(0)=0,求出a的值,然后验证即可.
解答 解:(Ⅰ)∵f(x)=ax-lnx,
∴函数的定义域为(0,+∞).
∴f′(x)=a-$\frac{1}{x}$=$\frac{ax-1}{x}$.
∵f(x)在x=$\frac{\sqrt{2}}{2}$处取得极值,
即f′($\frac{\sqrt{2}}{2}$)=a-$\sqrt{2}$=0,
∴a=$\sqrt{2}$.
当a=$\sqrt{2}$时,在(0,$\frac{\sqrt{2}}{2}$)内f′(x)<0,在($\frac{\sqrt{2}}{2}$,+∞)内f′(x)>0,
∴x=$\frac{\sqrt{2}}{2}$是函数y=f(x)的极值点.
∴a=$\sqrt{2}$.
故选:A
点评 本题主要考查了利用导数研究函数的极值,关键需要验证,属于基础题.

练习册系列答案
相关题目
6.若a=20.1,b=ln2,c=log0.36,则a,b,c的大小关系为( )
| A. | a>c>b | B. | c>b>a | C. | a>b>c | D. | b>c>a |
10.球的大圆面积扩大为原大圆面积的4倍,则球的表面积扩大成原球表面积的( )
| A. | 2倍 | B. | 4倍 | C. | 8倍 | D. | 16倍 |
7.数列2,5,10,17,…的第n项an可能为( )
| A. | 2n | B. | n2+n | C. | 2n-1 | D. | n2+1 |
4.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据涪陵气象局某日早6点至晚9点在李渡新城区、涪陵老城区两个地区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,李渡新城区、涪陵老城区浓度的方差较小的是( )
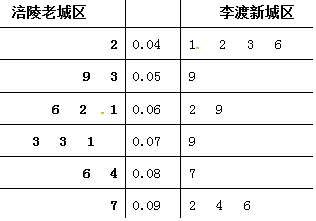

| A. | 李渡新城区 | B. | 涪陵老城区 | ||
| C. | 李渡新城区、涪陵老城区相等 | D. | 无法确定 |
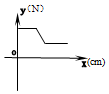
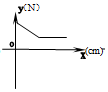
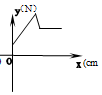
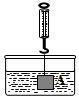 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则如图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )
在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则如图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )