题目内容
17.已知两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,则下列结论不正确的是( )| A. | $\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为cosθ | B. | $\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$ | ||
| C. | ($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$) | D. | |$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=1 |
分析 根据向量数量积公式以及模长公式分别分析选项即可.
解答 解:因为两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,所以$\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为|$\overrightarrow{{e}_{1}}$|cosθ=cosθ;故A正确;
$\overrightarrow{{e}_{1}^{2}}$=$\overrightarrow{{e}_{2}^{2}}$=|$\overrightarrow{{e}_{1}^{2}}$|=|$\overrightarrow{{e}_{2}^{2}}$|=1;故B正确;
($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•($\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$)=$\overrightarrow{{e}_{1}^{2}}$-$\overrightarrow{{e}_{2}^{2}}$=0;故C正确;
|$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$|=|$\overrightarrow{{e}_{1}}$|•|$\overrightarrow{{e}_{2}}$||cosθ|=|cosθ|≠1;故D错误;
故选D.
点评 本题考查了单位向量的性质;主要利用了平面向量的数量积公式.

练习册系列答案
相关题目
7.在△ABC中,已知sin(A+B)=$\frac{1}{2}$,则∠C是( )
| A. | 150° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
2.已知函数f(x)=axsinx-$\frac{3}{2}({a∈R})$,且在$[{0,\frac{π}{2}}]$上的最大值为$\frac{π-3}{2}$,则实数a的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
9.从甲、乙、丙等5名候选学生中选出2名作为校运动会志愿者,则甲、乙、丙中有2人被选中的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
6.若a=20.1,b=ln2,c=log0.36,则a,b,c的大小关系为( )
| A. | a>c>b | B. | c>b>a | C. | a>b>c | D. | b>c>a |
7.数列2,5,10,17,…的第n项an可能为( )
| A. | 2n | B. | n2+n | C. | 2n-1 | D. | n2+1 |
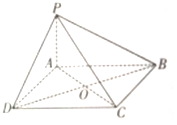 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.