题目内容
14.与椭圆$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1有公共焦点,且离心率e=$\frac{5}{3}$的双曲线方程是( )| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1 |
分析 求出椭圆的焦点坐标,得到双曲线的焦点坐标,利用双曲线的离心率,求出a,b,即可得到双曲线方程.
解答 解:椭圆$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1有公共焦点,双曲线的焦点坐标:(5,0),c=5,双曲线方程的离心率e=$\frac{5}{3}$,可得a=3,则b=4,与椭圆$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1有公共焦点,且离心率e=$\frac{5}{3}$的双曲线方程是:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1.
故选:A.
点评 本题考查椭圆的简单性质以及双曲线的简单性质的应用,双曲线法方程求法,考查计算能力.

练习册系列答案
相关题目
2.已知函数f(x)=axsinx-$\frac{3}{2}({a∈R})$,且在$[{0,\frac{π}{2}}]$上的最大值为$\frac{π-3}{2}$,则实数a的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
9.从甲、乙、丙等5名候选学生中选出2名作为校运动会志愿者,则甲、乙、丙中有2人被选中的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
19.函数y=xex的导函数y′=( )
| A. | xex | B. | ex | C. | (x+1)ex | D. | 1+ex |
6.若a=20.1,b=ln2,c=log0.36,则a,b,c的大小关系为( )
| A. | a>c>b | B. | c>b>a | C. | a>b>c | D. | b>c>a |
4.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据涪陵气象局某日早6点至晚9点在李渡新城区、涪陵老城区两个地区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,李渡新城区、涪陵老城区浓度的方差较小的是( )
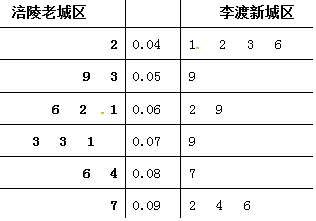

| A. | 李渡新城区 | B. | 涪陵老城区 | ||
| C. | 李渡新城区、涪陵老城区相等 | D. | 无法确定 |
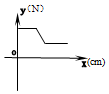
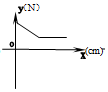
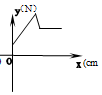
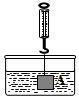 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则如图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )
在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则如图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )