题目内容
某商店经营一批进价为每件4元的商品,在市场调查时得到,此商品的销售单价x与日销售量y之间的一组数据满足:
=6.5,
=7,
(xi-
) (yi-
) =-11,
(xi-
) 2=5,则当销售单价x定为(取整数) 元时,日利润最大.
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
. |
| x |
考点:线性回归方程
专题:概率与统计
分析:根据已知中
=6.5,
=7,
(xi-
) (yi-
) =-11,
(xi-
) 2=5,求出回归直线方程,进而得到日利润的表达式,进而根据二次函数的图象和性质可估计日利润最大值.
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
. |
| x |
解答:
解:∵
(xi-
) (yi-
) =-11,
(xi-
) 2=5,
∴b=
=-
=-2.2,
将
=6.5,
=7代入得:a=
-b
=21.3,
故
关于
的回归方程为
=-2.2x+21.3,
故日利润的解析式为:Z=(-2.2x+21.3)(x-4)=-2.2x2+30.1x-85.2,
当x=
≈7时,日利润最大,
故答案为:7
| 5 |
 |
| i=1 |
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
. |
| x |
∴b=
| |||||||
|
| 11 |
| 5 |
将
. |
| x |
. |
| y |
. |
| y |
. |
| x |
故
 |
| y |
 |
| x |
 |
| y |
故日利润的解析式为:Z=(-2.2x+21.3)(x-4)=-2.2x2+30.1x-85.2,
当x=
| 30.1 |
| 2.2×2 |
故答案为:7
点评:统计也是高考新增的考点,回归直线方程的求法,又是统计中的一个重要知识点,其系数公式及性质要求大家要熟练掌握并应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将偶数按如图所示的规律排列下去,且用amn表示位于从上到下第m行,从左到右n列的数,比如a22=6,a43=18,若amn=2014,则有( )


| A、m=44,n=16 |
| B、m=44,n=29 |
| C、m=45,n=16 |
| D、m=45,n=29 |
定义:在数列{an}中,若满足
-
=d(n∈N+,d 为常数),称{an}为“等差比数列”.已知在“等差比数列”{an}中,a1=a2=1,a3=3,则
=( )
| an+2 |
| an+1 |
| an+1 |
| an |
| a2014 |
| a2012 |
| A、4×20122-1 |
| B、4×20132-1 |
| C、4×20142-1 |
| D、4×20132 |
已知
=(2,3),
=(-4,7),则
在
上的投影为( )
| a |
| b |
| b |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
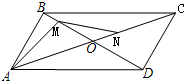 如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60°,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM=
如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60°,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM=