题目内容
已知函数f(x)=(x2+ax+b)ex在点(0,f(0))处的切线方程是y=-2x+1,其中e是自然对数的底数.
(Ⅰ) 求实数a、b的值;
(Ⅱ) 求函数f(x)在区间[-2,3]上的值域.
(Ⅰ) 求实数a、b的值;
(Ⅱ) 求函数f(x)在区间[-2,3]上的值域.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)先求出f(x)的导数f′(x),则f′(0)=-2和点(0,f(0))在直线y=-2x+1上,得出方程组,求出a、b的值.
(2)求出f(x)的导数,判断f(x)在区间[-2,3]上的单调性,再求出其值域.
(2)求出f(x)的导数,判断f(x)在区间[-2,3]上的单调性,再求出其值域.
解答:
解:(Ⅰ) 由f(x)=(x2+ax+b)ex,得f'(x)=[x2+(a+2)x+a+b]ex,
因为函数f(x)在点(0,f(0))处的切线方程是y=-2x+1,
所以
即
解得a=-3,b=1.(6分)
(Ⅱ)由(Ⅰ)知f(x)=(x2-3x+1)ex,f'(x)=(x2-x-2)ex=(x+1)(x-2)ex,(8分)
令f'(x)=0,得x1=-1或x2=2.f(x)与f'(x)的关系如下表:
由上表可知,函数f(x)在区间[-2,3]上的值域是[-e2,e3].(12分)
因为函数f(x)在点(0,f(0))处的切线方程是y=-2x+1,
所以
|
|
(Ⅱ)由(Ⅰ)知f(x)=(x2-3x+1)ex,f'(x)=(x2-x-2)ex=(x+1)(x-2)ex,(8分)
令f'(x)=0,得x1=-1或x2=2.f(x)与f'(x)的关系如下表:
| x | -2 | (-2,-1) | -1 | (-1,2) | 2 | (2,3) | 3 | ||
| f'(x) | + | 0 | - | 0 | + | ||||
| f(x) | 11e-2 | ↗ |
| ↘ | -e2 | ↗ | e3 |
点评:本题考查了导数在求切线上的应用,利用导数求函数要闭区间上的值域,是一道导数的综合题,属于中档题.

练习册系列答案
相关题目
已知圆M的一般方程为x2+y2-8x+6y=0,则下列说法中不正确的是( )
| A、圆M的圆心为(4,-3) |
| B、圆M被x轴截得的弦长为8 |
| C、圆M的半径为25 |
| D、圆M被y轴截得的弦长为6 |
半径为1cm,中心角为150°的角所对的弧长为( )cm.
A、
| ||
B、
| ||
C、
| ||
D、
|
关于x的二次方程(
•
)x2+4(
•
)x+(
•
)=0没有实数根,则向量
与
的夹角的范围为( )
| a |
| a |
| a |
| b |
| b |
| b |
| a |
| b |
A、[0,
| ||||
B、[0,
| ||||
C、(
| ||||
D、(
|
双曲线
-
=1的渐近线方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
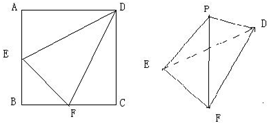 边长为2的正方形ABCD中,E∈AB,F∈BC
边长为2的正方形ABCD中,E∈AB,F∈BC 已知A,B是椭圆C:
已知A,B是椭圆C: