题目内容
已知函数f(x)=1-
,x∈(b-3,2b)是奇函数.
(1)求a,b的值;
(2)证明:f(x)是区间(b-3,2b)上的减函数;
(3)若f(m-1)+f(2m+1)>0,求实数m的取值范围.
| 5x•a |
| 5x+1 |
(1)求a,b的值;
(2)证明:f(x)是区间(b-3,2b)上的减函数;
(3)若f(m-1)+f(2m+1)>0,求实数m的取值范围.
考点:函数奇偶性的判断
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)由于函数f(x)是奇函数,且f(0)有意义,则f(0)=0,定义域关于原点对称,列出方程,即可得到a,b;
(2)运用单调性的定义,注意作差、变形,同时运用指数函数的单调性,即可判断符号,得到结论成立;
(3)运用奇函数的定义和函数f(x)是区间(-2,2)上的减函数,得到不等式组,注意定义域的运用,解出它们即可得到范围.
(2)运用单调性的定义,注意作差、变形,同时运用指数函数的单调性,即可判断符号,得到结论成立;
(3)运用奇函数的定义和函数f(x)是区间(-2,2)上的减函数,得到不等式组,注意定义域的运用,解出它们即可得到范围.
解答:
(1)解:∵函数f(x)=1-
,x∈(b-3,2b)是奇函数,
∴f(0)=1-
=0,且b-3+2b=0,
即a=2,b=1.
(2)证明:由( I)得f(x)=1-
=
,x∈(-2,2),
设任意 x1,x2∈(-2,2)且x1<x2,
∴f(x1)-f(x2)=
-
=
,
∵x1<x2∴5x1<5x2∴5x2-5x1>0
又∵5x1+1>0,5x2+1>0
∴
>0,∴f(x1)>f(x2).
∴f(x)是区间(-2,2)上的减函数.
(3)解:∵f(m-1)+f(2m+1)>0,
∴f(m-1)>-f(2m+1)
∵f(x)奇函数∴f(m-1)>f(-2m-1)
∵f(x)是区间(-2,2)上的减函数
∴
即有
∴-1<m<0,
则实数m的取值范围是(-1,0).
| a•5x |
| 5x+1 |
∴f(0)=1-
| a |
| 2 |
即a=2,b=1.
(2)证明:由( I)得f(x)=1-
| 2•5x |
| 5x+1 |
| 1-5x |
| 5x+1 |
设任意 x1,x2∈(-2,2)且x1<x2,
∴f(x1)-f(x2)=
| 1-5x1 |
| 5x1+1 |
| 1-5x2 |
| 5x2+1 |
| 2(5x2-5x1) |
| (5x1+1)(5x2+1) |
∵x1<x2∴5x1<5x2∴5x2-5x1>0
又∵5x1+1>0,5x2+1>0
∴
| 2(5x2-5x1) |
| (5x1+1)(5x2+1) |
∴f(x)是区间(-2,2)上的减函数.
(3)解:∵f(m-1)+f(2m+1)>0,
∴f(m-1)>-f(2m+1)
∵f(x)奇函数∴f(m-1)>f(-2m-1)
∵f(x)是区间(-2,2)上的减函数
∴
|
|
∴-1<m<0,
则实数m的取值范围是(-1,0).
点评:本题考查函数的性质和运用,考查函数的奇偶性和单调性的定义和判断,以及运用解不等式,注意定义域,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知圆M的一般方程为x2+y2-8x+6y=0,则下列说法中不正确的是( )
| A、圆M的圆心为(4,-3) |
| B、圆M被x轴截得的弦长为8 |
| C、圆M的半径为25 |
| D、圆M被y轴截得的弦长为6 |
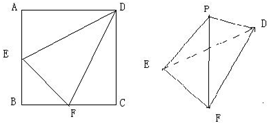 边长为2的正方形ABCD中,E∈AB,F∈BC
边长为2的正方形ABCD中,E∈AB,F∈BC 已知A,B是椭圆C:
已知A,B是椭圆C: