题目内容
在平面直角坐标系xOy中,已知椭圆
+
=1(a>b>0)过点(1,1).
(1)若椭圆的离心率为
,求椭圆的方程;
(2)若椭圆上两动点P,Q,满足OP⊥OQ.
①已知命题:“直线PQ恒与定圆C相切”是真命题,试直接写出圆C的方程;(不需要解答过程)
②设①中的圆C交y轴的负半轴于M点,二次函数y=x2-m的图象过点M.点A,B在该图象上,当A,O,B三点共线时,求△MAB的面积S的最小值.
| x2 |
| a2 |
| y2 |
| b2 |
(1)若椭圆的离心率为
| ||
| 2 |
(2)若椭圆上两动点P,Q,满足OP⊥OQ.
①已知命题:“直线PQ恒与定圆C相切”是真命题,试直接写出圆C的方程;(不需要解答过程)
②设①中的圆C交y轴的负半轴于M点,二次函数y=x2-m的图象过点M.点A,B在该图象上,当A,O,B三点共线时,求△MAB的面积S的最小值.
考点:椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)由e=
,得出a、b、c的关系,设出椭圆方程,把(1,1)代入方程,求出b2、a2即可;
(2)①由OP⊥OQ,且直线PQ恒与定圆C相切,得出圆C的方程为x2+y2=1;
②由题意知,二次函数y=x2-1,设直线AB的方程y=kx,由
,消去y,由根与系数的关系,求出x1+x2,x1x2;计算△MAB的面积S的最小值即可.
| ||
| 2 |
(2)①由OP⊥OQ,且直线PQ恒与定圆C相切,得出圆C的方程为x2+y2=1;
②由题意知,二次函数y=x2-1,设直线AB的方程y=kx,由
|
解答:
解:(1)由e=
,
则a:b:c=
:1:1;
∴可设椭圆方程为
+
=1,将(1,1)代入得
+
=1,
∴b2=
,a2=3,
∴椭圆方程为
+
=1;
(2)①根据题意,用特殊值来验证,如图所示;
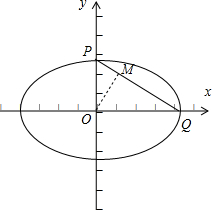
∵椭圆过点(1,1),
∴
+
=1,
即a2+b2=a2b2;
又OP⊥OQ,
∴|PQ|=
;
∴点O到直线PQ的距离|OM|=
=1;
∴根据椭圆的对称性,得出圆C的方程是x2+y2=1;
②由题意,二次函数为y=x2-1,
设直线AB的方程为y=kx,
由
,消去y得,x2-kx-1=0;
设A(x1,y1),B(x2,y2),则x1+x2=k,x1x2=-1,
则S=
OM•|x1-x2|=
=
;
当k=0时,△MAB的面积S的最小值为1.
| ||
| 2 |
则a:b:c=
| 2 |
∴可设椭圆方程为
| x2 |
| 2b2 |
| y2 |
| b2 |
| 1 |
| 2b2 |
| 1 |
| b2 |
∴b2=
| 3 |
| 2 |
∴椭圆方程为
| x2 |
| 3 |
| 2y2 |
| 3 |
(2)①根据题意,用特殊值来验证,如图所示;

∵椭圆过点(1,1),
∴
| 1 |
| a2 |
| 1 |
| b2 |
即a2+b2=a2b2;
又OP⊥OQ,
∴|PQ|=
| a2+b2 |
∴点O到直线PQ的距离|OM|=
| ab | ||
|
∴根据椭圆的对称性,得出圆C的方程是x2+y2=1;
②由题意,二次函数为y=x2-1,
设直线AB的方程为y=kx,
由
|
设A(x1,y1),B(x2,y2),则x1+x2=k,x1x2=-1,
则S=
| 1 |
| 2 |
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
| 1 |
| 2 |
| k2+4 |
当k=0时,△MAB的面积S的最小值为1.
点评:本题考查了直线与圆锥曲线的应用问题,解题时应根据题意,应用待定系数法求出圆锥曲线的方程,应用直线方程与圆锥曲线方程联立,求直线被圆锥曲线所截得的弦长的问题,是较难的题目.

练习册系列答案
相关题目
已知a>b>c,则下面式子一定成立的是( )
| A、ac>bc | ||||
| B、a-c>b-c | ||||
C、
| ||||
| D、a+c=2b |
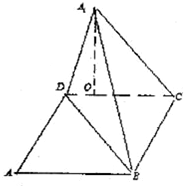 如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.
如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.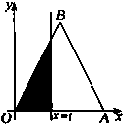 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则