题目内容
设i是虚数单位,
是复数z=
+
i的共轭复数,则z2•
=( )
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:直接利用复数代数形式的除法运算化简求值.
解答:
解:由z=
+
i,得
=
-
i,
∴z2•
=(z•
)•z=
•z=
+
i.
故选:A.
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
∴z2•
. |
| z |
. |
| z |
(
|
| 1 |
| 2 |
| ||
| 2 |
故选:A.
点评:本题考查复数代数形式的除法运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
使函数f(x)=
在(-∞,+∞)上是减函数的一个充分不必要条件是( )
|
A、
| ||||
B、0<a<
| ||||
C、
| ||||
D、0<a<
|
已知平面向量
=(2,3),
=(x,y),
-
=(1,7),则x,y的值分别是( )
| a |
| b |
| b |
| 2a |
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
已知a>b>c,则下面式子一定成立的是( )
| A、ac>bc | ||||
| B、a-c>b-c | ||||
C、
| ||||
| D、a+c=2b |
过抛物线y2=2px(p>0)的焦点作倾斜角为30°的直线l与抛物线交于P、Q两点,分别过P、Q两点作PP1,QQ1垂直于抛物线的准线于P1、Q1,若|PQ|=2,则四边形PP1Q1Q的面积是( )
A、
| ||
| B、2 | ||
| C、3 | ||
| D、1 |
方程3x+1-x=6的解所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
已知边长为1的正三角形ABC,D是BC的中点,E是AC上一点且AE=2EC.则
•
=( )
| AD |
| BE |
A、
| ||
B、-
| ||
| C、0 | ||
| D、4 |
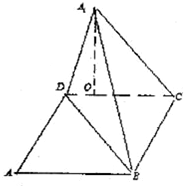 如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.
如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.