题目内容
19.圆心在直线5x-3y=8上,又与两坐标轴相切的圆的方程是(x-4)2+(y-4)2=16和(x-1)2+(y+1)2=1.分析 与坐标轴相切,所以圆心到两个坐标轴距离相等,结合圆心在5x-3y=8上,求出圆心坐标,可得圆的半径,从而可得圆的标准方程.
解答 解:与坐标轴相切,所以圆心到两个坐标轴距离相等,所以x=y或x=-y
又圆心在5x-3y=8上
若x=y,则x=y=4;若x=-y,则x=1,y=-1
所以圆心是(4,4)或(1,-1)
因为半径就是圆心到切线距离,即到坐标轴距离
所以圆心是(4,4),则r=4;圆心是(1,-1),则r=1
所以所求圆的标准方程为(x-4)2+(y-4)2=16和(x-1)2+(y+1)2=1.
故答案为:(x-4)2+(y-4)2=16和(x-1)2+(y+1)2=1.
点评 本题考查圆的标准方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.已知$\overrightarrow a=(-3,4),\overrightarrow b=(-2,1)$,则$\overrightarrow a$在$\overrightarrow b$上的投影为( )
| A. | -2 | B. | 2 | C. | $-2\sqrt{5}$ | D. | $2\sqrt{5}$ |
4.在△ABC中,内角A,B,C的对边分别是a,b,c,若bcosC=(2a-c)cosB,则B=( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
6.已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f($\frac{π}{6}$)|对x∈R恒成立,且f($\frac{π}{2}$)>f(π),则f(x)的单调递增区间是( )
| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | B. | [kπ,kπ+$\frac{π}{2}$](k∈Z) | C. | [kπ-$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | D. | [kπ-$\frac{π}{2}$,kπ](k∈Z) |
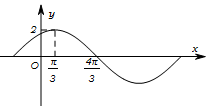 已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示. ,∠C=
,∠C= ,则∠A=_______.
,则∠A=_______.