题目内容
关于x的不等式sin2x+acosx-a2≤1+cosx对一切x∈R恒成立,则实数a的取值范围为( )
A、(-1,
| ||
B、[-1,
| ||
C、(-∞,-1]∪[
| ||
D、(-∞,-1)∪(
|
考点:函数恒成立问题
专题:函数的性质及应用
分析:将不等式进行转化,利用换元法将函数转化为一元二次函数,根据一元二次函数的性质建立不等式关系即可得到结论.
解答:
解:不等式等价为1-cos2x+acosx-a2≤1+cosx对一切x∈R恒成立,
即cos2x+(1-a)cosx+a2≥0恒成立,
设t=cosx,则-1≤t≤1,
则不等式等价为t2+(1-a)t+a2≥0,在-1≤t≤1上恒成立,
设f(t)=t2+(1-a)t+a2,-1≤t≤1,
对称性t=-
=
,
则满足
.即
,
则
,
即
,解得a≤-1或a≥
,
故选:C
即cos2x+(1-a)cosx+a2≥0恒成立,
设t=cosx,则-1≤t≤1,
则不等式等价为t2+(1-a)t+a2≥0,在-1≤t≤1上恒成立,
设f(t)=t2+(1-a)t+a2,-1≤t≤1,
对称性t=-
| 1-a |
| 2 |
| a-1 |
| 2 |
则满足
|
|
则
|
即
|
| 1 |
| 3 |
故选:C
点评:此题考查函数的恒成立问题,利用换元法结合一元二次不等式和一元二次函数的性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
观察以下不等式:1>
;1+
+
>1;1+
+
…+
>
;1+
+
+…+
>2;1+
+
+…+
>
;由此推测第n个不等式为( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 7 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 31 |
| 5 |
| 2 |
A、1+
| ||||||||
B、1+
| ||||||||
C、1+
| ||||||||
D、1+
|
已知点M与两个定点(1,0),(-2,0)的距离的比为
,则点M的轨迹所包含的图形面积等于( )
| 1 |
| 2 |
| A、9π | B、8π | C、4π | D、π |
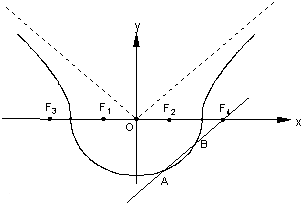 如图,曲线Γ由曲线
如图,曲线Γ由曲线