题目内容
已知点N(4,0),圆M:(x+4)2+y2=4,点A是圆M上一个动点,线段AN的垂直平分线交直线AM于点P,则点P的轨迹方程为 .
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:|PN|-|PM|=|PA|-|PM|=|MA|=2,可得点P的轨迹是M,N为焦点,以2为实轴长的双曲线.可得结论.
解答:
解:由已知,得|PN|=|PN|,所以|PN|-|PM|=|PA|-|PM|=|MA|=2
又|MN|=8,2<8,
根据双曲线的定义,点P的轨迹是M,N为焦点,以2为实轴长的双曲线,
所以2a=2,2c=8,所以b=
,
所以,点P的轨迹方程为:x2-
=1.
故答案为:x2-
=1.
又|MN|=8,2<8,
根据双曲线的定义,点P的轨迹是M,N为焦点,以2为实轴长的双曲线,
所以2a=2,2c=8,所以b=
| 15 |
所以,点P的轨迹方程为:x2-
| y2 |
| 15 |
故答案为:x2-
| y2 |
| 15 |
点评:本题主要考查了轨迹方程的问题,解题的关键是利用了双曲线的定义求得轨迹方程.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
函数y=(
)x-
的图象可能是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、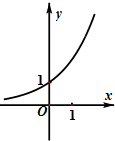 |
B、 |
C、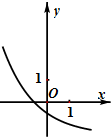 |
D、 |
阅读如图程序框图,下列说法正确的是( )
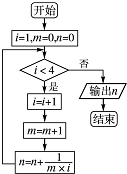

| A、该框图只含有顺序结构、条件结构 |
| B、该框图只含有顺序结构、循环结构 |
| C、该框图只含有条件结构、循环结构 |
| D、该框图包含顺序结构、条件结构、循环结构 |

 如图,一个广告气球被一束入射角为30°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则制作这个广告气球至少需要的面料是
如图,一个广告气球被一束入射角为30°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则制作这个广告气球至少需要的面料是