题目内容
已知双曲线C:
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相交,则双曲线C离心率的取值范围是 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先根据双曲线方程求得双曲线的渐近线,进而利用圆心到渐近线的距离小于半径求得a和b的关系,进而利用c2=a2+b2求得a和c的关系,则双曲线的离心率可求.
解答:
解:∵双曲线渐近线为bx±ay=0,与圆(x-2)2+y2=1相交
∴圆心到渐近线的距离小于半径,即
<1
∴3b2<a2,
∴c2=a2+b2<
a2,
∴e=
<
∵e>1
∴1<e<
.
故答案为:(1,
)
∴圆心到渐近线的距离小于半径,即
| 2b | ||
|
∴3b2<a2,
∴c2=a2+b2<
| 4 |
| 3 |
∴e=
| c |
| a |
2
| ||
| 3 |
∵e>1
∴1<e<
2
| ||
| 3 |
故答案为:(1,
2
| ||
| 3 |
点评:本题主要考查了双曲线的简单性质,直线与圆的位置关系,点到直线的距离公式等.考查了学生数形结合的思想的运用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=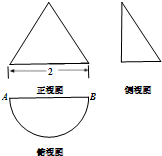 一个几何体的三视图如图所示,其中正视图是等边三角形,俯视图是半圆.现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点,则蚂蚁所经过路程的最小值为
一个几何体的三视图如图所示,其中正视图是等边三角形,俯视图是半圆.现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点,则蚂蚁所经过路程的最小值为
 如图,一个广告气球被一束入射角为30°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则制作这个广告气球至少需要的面料是
如图,一个广告气球被一束入射角为30°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则制作这个广告气球至少需要的面料是