题目内容
17.已知数列{an}满足a1=0,an+1=$\frac{{a}_{n}-\sqrt{3}}{{\sqrt{3}a}_{n}+1}$(n∈N*),则a2010=( )| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | 3 |
分析 根据题意,由数列的递推公式写出数列的前几项,分析可得an+3=an,进而分析可得a2010=a3,即可得答案.
解答 解:根据题意,若a1=0,a2=$\frac{-\sqrt{3}}{1}$=-$\sqrt{3}$.
a3=$\frac{-2\sqrt{3}}{-3+1}$=$\sqrt{3}$,a4=$\frac{\sqrt{3}-\sqrt{3}}{3+1}$=0,a5=$\frac{-\sqrt{3}}{1}$=-$\sqrt{3}$,…,
由此可知,an+3=an.
又2 010=3×670,
所以a2010=a3=$\sqrt{3}$.
故选:C.
点评 本题考查数列的递推公式,关键是写出数列的前几项,分析得到规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.函数y=x2cosx的导数为( )
| A. | y′=x2cosx-2xsin x | B. | y′=2xcos x+x2sin x | ||
| C. | y′=2xcosx-x2sinx | D. | y′=xcosx-x2sin x |
9.若函数f(x)=x2+bx+c的图象的对称轴为x=2,则函数f(x)的导函数f'(x)的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第三象限 |
6.已知f(x)=x3+x2f′(2)+2lnx,则f′(1)=( )
| A. | $\frac{3}{2}$ | B. | $-\frac{11}{3}$ | C. | 3 | D. | -3 |
7.函数f(x)的导函数f′(x)的图象如图所示,则( )
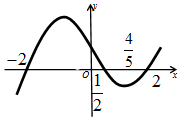

| A. | $\frac{1}{2}$为f(x)的极大值点 | B. | -2为f(x)的极大值点 | ||
| C. | 2为f(x)的极大值 | D. | $\frac{4}{5}$为f(x)的极小值点 |
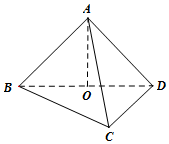 (文科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,
(文科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,