题目内容
2.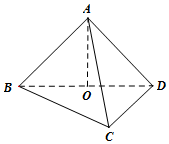 (文科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,
(文科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,
求(1)AC与平面BCD所成角的大小;
(2)异面直线AB和CD的大小.
分析 (1)因为A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,所以OA是三棱锥的高,在直角三角形AOC中可计算AO,再由OA⊥平面BCD,知∠ACO是AC与平面BCD所成角,由此能求出AC与平面BCD所成角的大小.
(2)取BC中点F,AC中点E,利用三角形中位线定理证明∠EFO即为异面直线AB和CD所成的角,再在△EFO中分别计算三边的长,利用解直角三角形知识即可求得此角.
解答 解:(1)∵A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,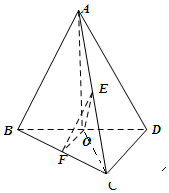
∴OA是三棱锥的高
∵BC=1,CD=$\sqrt{2}$.
∴OC=OB=OD=$\frac{\sqrt{3}}{2}$,OA=$\sqrt{A{C}^{2}-O{C}^{2}}$=$\frac{1}{2}$,
∵OA⊥平面BCD,∴∠ACO是AC与平面BCD所成角,
∵tan∠ACO=$\frac{AO}{CO}$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$,∴∠ACO=30°,
∴AC与平面BCD所成角为30°.
(2)如图,取BC中点F,AC中点E,连接EF,OE,OF
∵EF∥AB,OF∥CD
∴∠EFO即为异面直线AB和CD所成的角
在△EFO中,EF=$\frac{AB}{2}$=$\frac{\sqrt{A{O}^{2}+O{B}^{2}}}{2}$=$\frac{\sqrt{\frac{1}{4}+\frac{3}{4}}}{2}$=$\frac{1}{2}$,
OF=$\frac{CD}{2}=\frac{\sqrt{2}}{2}$,OE=$\frac{AC}{2}=\frac{\sqrt{A{O}^{2}+O{C}^{2}}}{2}$=$\frac{\sqrt{\frac{1}{4}+\frac{3}{4}}}{2}$=$\frac{1}{2}$,
∴∠FEO=90°,∠EFO=45°
∴异面直线AB和CD所成的角的大小为45°.
点评 本题考查线面角的求法,考查异面直线所成角的求法,考查推理论证能力、运算求解能力,考查整体思想、转化化归思想,考查数据处理能力和运用意识,是中档题.

| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | 3 |
| A. | 2 | B. | $\frac{2}{3}$ | C. | -$\frac{2}{3}$ | D. | -2 |