题目内容
18.已知$α∈(\frac{π}{2},π)$,且1+tanα≥0,则角α的取值范围是[$\frac{3π}{4}$,π).分析 根据1+tanα≥0求出-$\frac{π}{4}$+kπ≤α<$\frac{π}{2}$+kπ,k∈Z;再根据α∈($\frac{π}{2}$,π)求出α的取值范围.
解答 解:1+tanα≥0,
∴tanα≥-1,
解得-$\frac{π}{4}$+kπ≤α<$\frac{π}{2}$+kπ,k∈Z;
又α∈($\frac{π}{2}$,π),
∴取$\frac{3π}{4}$≤α<π,
即α的取值范围是[$\frac{3π}{4}$,π).
故答案为:[$\frac{3π}{4}$,π).
点评 本题考查了正切函数的图象与性质的应用问题,是基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
9.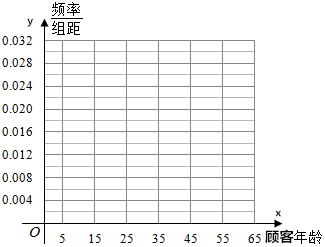 某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
(1)在表中作出这些数据的频率分布直方图;
(2)根据(1)中的频率分布直方图,求这100名顾客年龄的平均数;
(3)用分层抽样的方法从这100名顾客中抽取25人,再从抽取的25人中随机抽取2人,求年龄在[25,35)内的顾客人数X的分布列与数学期望.
 某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:| 顾客年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 频数 | 4 | 24 | 32 | 20 | 16 | 4 |
(2)根据(1)中的频率分布直方图,求这100名顾客年龄的平均数;
(3)用分层抽样的方法从这100名顾客中抽取25人,再从抽取的25人中随机抽取2人,求年龄在[25,35)内的顾客人数X的分布列与数学期望.
8.已知x,y是正数,且$\frac{1}{x}+\frac{9}{y}=1$,则x+y的最小值是( )
| A. | 6 | B. | 12 | C. | 16 | D. | 24 |