题目内容
10．若Sn等差数列{an}的前n项和，且a3=2，a8=10，则S10=60．分析 方法一：由已知条件可得数列的首项和公差，代入求和公式可得．
方法二：根据等差数列的性质和前n项和公式即可求出．
解答 解：方法一：由题意可得数列{an}的公差d=$\frac{{a}_{8}-{a}_{3}}{8-3}$=$\frac{10-2}{5}$=$\frac{8}{5}$，
故可得a1=a3-2d=2-2×$\frac{8}{5}$=-$\frac{6}{5}$
代入求和公式可得S10=10×（-$\frac{6}{5}$）+$\frac{10（10-1）}{2}$×$\frac{8}{5}$=60，
方法二：S10=$\frac{10（{a}_{1}+{a}_{10}）}{2}$=5（a3+a8）=5×12=60，
故答案为：60
点评 本题考查等差数列的前n项和，求出数列的首项和公差是解决问题的关键，属基础题．
练习册系列答案
相关题目
1．已知双曲线与椭圆$\frac{x^2}{9}+\frac{y^2}{25}=1$的焦点相同，且它们的离心率的乘积等于$\frac{8}{5}$，则此双曲线的方程为（ ）
| A． | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B． | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | C． | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D． | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
2．
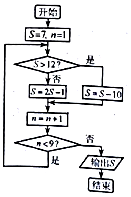阅读右边的程序框图，运行相应的程序，则输出的S值为（ ）
阅读右边的程序框图，运行相应的程序，则输出的S值为（ ）| A． | 3 | B． | 5 | C． | 9 | D． | 13 |