题目内容
函数y=sin(2x+
)是( )
| 5π |
| 2 |
| A、周期为π的奇函数 | ||
| B、周期为π的偶函数 | ||
C、周期为
| ||
D、周期为
|
考点:正弦函数的对称性,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:由条件利用诱导公式以及余弦函数的周期性和奇偶性,可得结论.
解答:
解:由于函数y=sin(2x+
)=sin(2x+
)=cos2x,故此函数是周期为
=π的偶函数,
故选:B.
| 5π |
| 2 |
| π |
| 2 |
| 2π |
| 2 |
故选:B.
点评:本题主要考查诱导公式以及余弦函数的周期性和奇偶性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知-1,x,-4成等比数列,则x的值为( )
| A、2 | ||||
B、-
| ||||
| C、2 或-2 | ||||
D、-
|
已知sinx+siny=
,则u=sinx+cos2x的最小值是( )
| 1 |
| 3 |
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|
[x]表示不超过x的最大整数,函数f(x)=|x|-[x]
①f(x)的定义域为R;
②f(x)的值域为(0,1];
③f(x)是偶函数;
④f(x)不是周期函数;
⑤f(x)的单调增区间为(k,k+1)(k∈N).
上面的结论正确的个数是( )
①f(x)的定义域为R;
②f(x)的值域为(0,1];
③f(x)是偶函数;
④f(x)不是周期函数;
⑤f(x)的单调增区间为(k,k+1)(k∈N).
上面的结论正确的个数是( )
| A、3 | B、2 | C、1 | D、0 |
已知双曲线
-
=1的实轴长、虚轴长、焦距依次成等比数列,则其离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
命题p:x(x-3)=0,命题q:x=3,则命题p是命题q的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
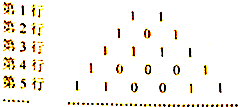 将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是
将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是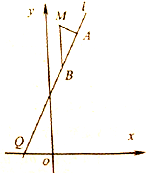 如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=
如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=