题目内容
若f(x)=
,则f(
)•f(-100)=( )
|
| π |
| 4 |
| A、-2 | B、-1 | C、1 | D、2 |
考点:函数的值
专题:函数的性质及应用
分析:利用分类函数的性质求解.
解答:
解:∵f(x)=
,
∴f(
)•f(-100)=tan
•lg100=2.
故选:D.
|
∴f(
| π |
| 4 |
| π |
| 4 |
故选:D.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意分段函数的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知m=a+
(a>2),n=2 2-b2(b≠0),则m,m的大小关系是( )
| 1 |
| a-2 |
| A、m>n | B、m<n |
| C、m=n | D、不确定 |
已知双曲线
-
=1的实轴长、虚轴长、焦距依次成等比数列,则其离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合M={x|2x≥1},N={x||x|≤2},则M∪N=( )
| A、[1,2] |
| B、[0,2] |
| C、[-2,+∞) |
| D、[0,+∞) |
设集合A={0,1},B={-1,0,m-2},若A⊆B,则实数m=( )
| A、0 | B、1 | C、2 | D、3 |
若函数f(x)=
x2-ax+lnx存在垂直于y轴的切线,则实数a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,-2]∪[2,+∞) |
| B、(-∞,-2)∪(2,+∞) |
| C、[2,+∞) |
| D、(2,+∞) |
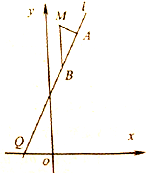 如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=
如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=