题目内容
 如图,在棱长为1的直三棱柱ABC-A1B1C1中,M为棱A1B1的中点,试求:
如图,在棱长为1的直三棱柱ABC-A1B1C1中,M为棱A1B1的中点,试求:(1)三棱锥M-ABC的体积;
(2)直线MC与BB1所成角的大小(结果用反三角函数值表示).
考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)由已知得AA1⊥底面ABC,AA1=1,S△ABC=
×1×1×sin60°=
,由此能求出三棱锥M-ABC的体积.
(2)以A为原点,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出直线MC与BB1所成角的大小.
| 1 |
| 2 |
| ||
| 4 |
(2)以A为原点,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出直线MC与BB1所成角的大小.
解答:
 解:(1)在棱长为1的直三棱柱ABC-A1B1C1中,
解:(1)在棱长为1的直三棱柱ABC-A1B1C1中,
∵AA1⊥底面ABC,AA1=1,
S△ABC=
×1×1×sin60°=
,
∴三棱锥M-ABC的体积:
V=
×AA1×S△ABC=
×1×
=
.
(2)以A为原点,AC为y轴,AA1为z轴,
建立空间直角坐标系,
则M(
,
,1),C(0,2,0),
B(
,
,0),B1(
,
,1),
=(-
,
,-1),
=(0,0,1),
|cos<
,
>|=|
|=
.
∴直线MC与BB1所成角的大小为arccos
.
 解:(1)在棱长为1的直三棱柱ABC-A1B1C1中,
解:(1)在棱长为1的直三棱柱ABC-A1B1C1中,∵AA1⊥底面ABC,AA1=1,
S△ABC=
| 1 |
| 2 |
| ||
| 4 |
∴三棱锥M-ABC的体积:
V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
(2)以A为原点,AC为y轴,AA1为z轴,
建立空间直角坐标系,
则M(
| ||
| 4 |
| 1 |
| 4 |
B(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| MC |
| ||
| 4 |
| 7 |
| 4 |
| BB1 |
|cos<
| MC |
| BB1 |
| -1 | ||||||
|
2
| ||
| 17 |
∴直线MC与BB1所成角的大小为arccos
2
| ||
| 17 |
点评:本题考查三棱锥的体积的求法,考查异面直线所成的角的大小的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
[x]表示不超过x的最大整数,函数f(x)=|x|-[x]
①f(x)的定义域为R;
②f(x)的值域为(0,1];
③f(x)是偶函数;
④f(x)不是周期函数;
⑤f(x)的单调增区间为(k,k+1)(k∈N).
上面的结论正确的个数是( )
①f(x)的定义域为R;
②f(x)的值域为(0,1];
③f(x)是偶函数;
④f(x)不是周期函数;
⑤f(x)的单调增区间为(k,k+1)(k∈N).
上面的结论正确的个数是( )
| A、3 | B、2 | C、1 | D、0 |
已知等差数列{an}的前n项和Sn,满足Sn=-
n2+2n,则Sn的最大值为( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
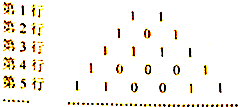 将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是
将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是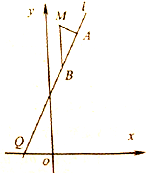 如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=
如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=