题目内容
设双曲线
-
=1（a＞0）的渐近线方程为3x±2y=0，则
（
）dx的值为（ ）
| x2 |
| a2 |
| y2 |
| 9 |
| ∫ | a 1 |
| 1 |
| x |
| A、ln2 | B、0 | C、ln3 | D、1 |
考点：双曲线的简单性质,定积分
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线
-
=1（a＞0）的渐近线方程为3x±2y=0，求出a，再计算
（
）dx的值．
| x2 |
| a2 |
| y2 |
| 9 |
| ∫ | a 1 |
| 1 |
| x |
解答：
解：∵双曲线
-
=1（a＞0）的渐近线方程为3x±2y=0，
∴
=
，
∴a=2，
∴
（
）dx=lnx
=ln2-ln1=ln2．
故选：A．
| x2 |
| a2 |
| y2 |
| 9 |
∴
| 3 |
| a |
| 3 |
| 2 |
∴a=2，
∴
| ∫ | a 1 |
| 1 |
| x |
| | | 2 1 |
故选：A．
点评：本题考查双曲线的性质，考查定积分知识，确定a的值是关键．
练习册系列答案
阅读快车系列答案
相关题目
若向量
=（1，1-x），
=（1，1+x），则函数f（x）=
是（ ）
| a |
| b |
| ||||||
| 4-|x-4| |
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、减函数 |
从2名男生和2名女生中，任意选择两人在星期六、星期日参加某公益活动，每天一人，则星期六安排一名男生、星期日安排一名女生的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知实数x∈[1，10]，执行如图所示的程序框图，则输出x的值不小于55的概率为（ ）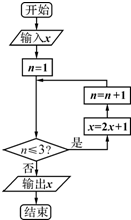
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f（x）的导函数为f′（x），若对任意x∈R都有f′（x）＞f（x）成立，则（ ）
| A、f（ln2014）＜2014f（0） |
| B、f（ln2014）=2014f（0） |
| C、f（ln2014）＞2014f（0） |
| D、f（ln2014）与2014f（0）的大小关系不确定 |
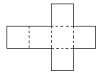如图是一个正方体纸盒的展开图，把1、-1、2、-2、