题目内容
已知函数f(x)=
,若f(a)=-
,则a的值为 .
|
| 5 |
| 4 |
考点:函数的值
专题:函数的性质及应用
分析:根据函数f(x)的解析式,讨论a>1、a≤1时,f(a)=-
,求出对应a的值.
| 5 |
| 4 |
解答:
解:∵函数f(x)=
,
且f(a)=-
,
∴当a>1时,f(a)=a3=-
,
解得a=-
,不满足题意,舍去;
当a≤1时,f(a)=-a2+2a=-
,
解得a=-
或a=
,
a=
时不满足题意,应舍去;
∴a的值为-
.
故答案为:-
.
|
且f(a)=-
| 5 |
| 4 |
∴当a>1时,f(a)=a3=-
| 5 |
| 4 |
解得a=-
| |||
| 2 |
当a≤1时,f(a)=-a2+2a=-
| 5 |
| 4 |
解得a=-
| 1 |
| 2 |
| 5 |
| 2 |
a=
| 5 |
| 2 |
∴a的值为-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了分段函数的应用问题,解题时应对自变量的取值范围进行讨论,是基础题目.

练习册系列答案
相关题目
“m=-2”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( )
| A、充分必要条件 |
| B、充分而不必要条件 |
| C、必要而不充分条件 |
| D、既不充分也不必要条件 |
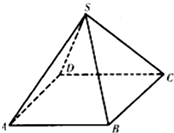 如图,四棱锥S-ABCD的底面是边长为2a的菱形,且SA=SC=2a,SB=SD=
如图,四棱锥S-ABCD的底面是边长为2a的菱形,且SA=SC=2a,SB=SD=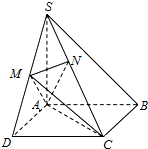 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.