题目内容
某旅馆有三人间、两人间、单人间三种房间各一间,有3位成人带2个小孩来住宿,小孩必须有成人陪同,则不同的住宿方法有( )
| A、18种 | B、21种 |
| C、27种 | D、35种 |
考点:计数原理的应用
专题:应用题,排列组合
分析:由题意小孩的住法可以分为两类,一类是全住三人间,有一大人陪同,一类是三人间与两人间各一,由计数原理得出每一类的住宿方法即可.
解答:
解:若小孩全住三人间,则需要选出一个大人陪同且另外两个大人可能住双人间,也可能各住一间,故住宿方法有C31×(1+A22)=9种
若小孩一住三人间一住两人间,则大人的住法有二,一是两位大人住三人间,另一人住双人间,二是一位大人住三人间,另两位大人各住一间,故住宿方法有A22×(C32+C31×A22)=18种
故不同的安排方法有9+18=27种.
故选:C.
若小孩一住三人间一住两人间,则大人的住法有二,一是两位大人住三人间,另一人住双人间,二是一位大人住三人间,另两位大人各住一间,故住宿方法有A22×(C32+C31×A22)=18种
故不同的安排方法有9+18=27种.
故选:C.
点评:本题考查计数原理的应用,求解本题的关键是正确分类,理清符合实际情况的安排方法并选择恰当的计数方法计算所有的种数.本题易因分不清符合情况的安排方法有哪些而导致错误或解答不出,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)=|x+2|+|x-4|的最小值为n,则(x-
)n的展开式中常数项为( )
| 2 |
| x |
| A、-160 | B、-20 |
| C、20 | D、160 |
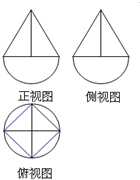 某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||||
B、5+
| ||||
C、5+
| ||||
D、
|
复数
在复平面内所对应的点在实轴上,那么实数a=( )
| a+i |
| 2-i |
| A、-2 | B、0 | C、1 | D、2 |
已知tan2α=
,α∈(0,
),则
=( )
| 3 |
| 4 |
| π |
| 4 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |
现有1位教师,2位男同学,3位女同学共6人站成一排,要求2位男同学站两边,3位女同学中有且仅有两位相邻,则不同排法有( )
| A、12种 | B、24种 |
| C、36种 | D、72种 |
某几何体的三视图如图所示,则该几何体的表面积为( )


| A、20π | B、16π |
| C、12π | D、10π |