题目内容
(文)长度为6的动弦AB在抛物线y2=4x上滑动,AB中点到y轴距离的最小值为2,则直线AB的斜率为( )
| A、± | ||
B、±
| ||
C、±
| ||
| D、±2 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由抛物线定义,知弦AB的中点M到Y轴的距离最短时弦AB过焦点,由此设出直线AB的方程,用代数法结合椭圆的弦长公式能求出结果.
解答:
解:∵长度为6的动弦AB在抛物线y2=4x上滑动,AB中点到y轴距离的最小值为2,
∴AB过抛物线y2=4x的焦点F(1,0),
设AB的方程为y=k(x-1),并代入抛物线y2=4x,
得k2(x-1)2=4x,
整理,得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),则x1+x2=2+
,x1x2=1,
∵|AB|=6,
∴6=
,
整理,得5k4-8k2-4=0,
解得k2=2,或k2=-
(舍)
∴k=±
.
故选:C.
∴AB过抛物线y2=4x的焦点F(1,0),
设AB的方程为y=k(x-1),并代入抛物线y2=4x,
得k2(x-1)2=4x,
整理,得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),则x1+x2=2+
| 4 |
| k2 |
∵|AB|=6,
∴6=
(1+k2)[(2+
|
整理,得5k4-8k2-4=0,
解得k2=2,或k2=-
| 2 |
| 5 |
∴k=±
| 2 |
故选:C.
点评:本题考查直线的斜率的求法,是中档题,解题时要熟练掌握抛物线性质,注意弦长公式的合理运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
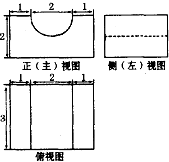
已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )

A、24-
| ||
B、24-
| ||
| C、24-π | ||
D、24-
|
已知定义在R上的奇函数f(x),且为减函数,又知f(1-a)+f(1-a2)<0,则a的取值范围为( )
| A、(-2,1) |
| B、(-∞,-2)∪(1,+∞) |
| C、(0,1) |
| D、(0,2) |
若n<m<0,则
-
等于( )
| m2+2mn+n2 |
| m2-2mn+n2 |
| A、2m | B、2n |
| C、-2m | D、-2n |
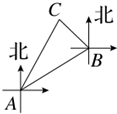 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.A、5(
| ||||
B、5(
| ||||
C、10(
| ||||
D、10(
|