题目内容
已知U=R,集合A={x|y=
+ln(x+3)},B={y|y=lg(2x-x2)},则A∩(∁UB)=( )
| 1 |
| x-1 |
| A、(0,1) |
| B、(1,+∞) |
| C、(0,1)∪(1,+∞) |
| D、(-3,0] |
考点:交、并、补集的混合运算
专题:集合
分析:先将集合A,B化简,然后求出∁UB,再与A求交集.
解答:
解:由题意A={x|y=
+ln(x+3)}={x|x-1≠0,且x+3>0}=(-3,1)∪(1,+∞),
B={y|y=lg(2x-x2)}为函数y=lg(2x-x2)值域,此时2x-x2∈(0,1],B=(-∞,0],
则∁UB=(0,+∞),
A∩(∁UB)=(0,1)∪(1,+∞),
故选:C.
| 1 |
| x-1 |
B={y|y=lg(2x-x2)}为函数y=lg(2x-x2)值域,此时2x-x2∈(0,1],B=(-∞,0],
则∁UB=(0,+∞),
A∩(∁UB)=(0,1)∪(1,+∞),
故选:C.
点评:本题考察集合的交并补运算,注意集合的表示使用的是描述法,集合A为定义域,而集合B是值域.

练习册系列答案
相关题目
函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数,则实数a的范围是( )
| A、a≤-3 | B、a≤5 |
| C、a≥3 | D、a≥5 |
在下列关于点P,直线l、m与平面α、β的命题中,正确的是( )
| A、若m⊥α,l⊥m,则l∥α |
| B、若α⊥β,α∩β=m,P∈α,P∈l,且l⊥m,则l⊥β |
| C、若l,m是异面直线,m?α,m∥β,l?β,l∥α,则α∥β |
| D、若α⊥β,且l⊥β,m⊥l,则m⊥α |
数列3,7,13,21,31,…的一个通项公式是( )
| A、an=4n-1 |
| B、an=n2+n+1 |
| C、an=2+2n-n2 |
| D、an=n(n2-1) |
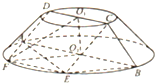 如图所示,圆台上、下底面半径分别为4,8,母线与底面所成角为45°,平面ABCD为圆台的轴截面,E为下底面圆弧上一点,且∠ABE=60°,过CDE的平面交⊙O2于点F.
如图所示,圆台上、下底面半径分别为4,8,母线与底面所成角为45°,平面ABCD为圆台的轴截面,E为下底面圆弧上一点,且∠ABE=60°,过CDE的平面交⊙O2于点F.