题目内容
设F1是椭圆x2+
=1的下焦点,O为坐标原点,点P在椭圆上,则
•
的最大值为 .
| y2 |
| 4 |
| PF1 |
| PO |
考点:椭圆的简单性质,平面向量数量积的运算
专题:平面向量及应用,圆锥曲线的定义、性质与方程
分析:根据椭圆的标准方程求出F1的坐标(0,-
),设P(x,y),所以可求出向量
,
的坐标,所以结合点P满足椭圆的方程,可求出
•
=(
y+1)2,而y∈[-2,2],所以y=2时
•
取到最大值,所以将y=2带入即可求出该最大值.
| 3 |
| PF1 |
| PO |
| PF1 |
| PO |
| ||
| 2 |
| PF1 |
| PO |
解答:
解:根据椭圆的标准方程知F1(0,-
),设P(x,y),则:
•
=(-x,-
-y)•(-x,-y)=x2+
y+y2=1-
+
y+y2=
y2+
y+1=(
y+1)2;
又-2≤y≤2;
∴y=2时,
•
取最大值4+2
.
故答案为:4+2
.
| 3 |
| PF1 |
| PO |
| 3 |
| 3 |
| y2 |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| ||
| 2 |
又-2≤y≤2;
∴y=2时,
| PF1 |
| PO |
| 3 |
故答案为:4+2
| 3 |
点评:考查椭圆的标准方程,椭圆的焦点,以及向量数量积的坐标运算,以及观察法求二次函数的最值.

练习册系列答案
相关题目
设集合A={3,5,6,8},B={4,5,7,8},则A∩B=( )
| A、{3,5,8} |
| B、{5,8} |
| C、{5,7,8} |
| D、∅ |
将直线l:x-y+1=0绕着点A(2,3)逆时针方向旋转90°,得到直线l1的方程是( )
| A、x-2y+4=0 |
| B、x+y-1=0 |
| C、x+y-5=0 |
| D、2x+y-7=0 |
已知U=R,集合A={x|y=
+ln(x+3)},B={y|y=lg(2x-x2)},则A∩(∁UB)=( )
| 1 |
| x-1 |
| A、(0,1) |
| B、(1,+∞) |
| C、(0,1)∪(1,+∞) |
| D、(-3,0] |
函数f(x)=x3-ax+1在区间[2,+∞)内是增函数,则实数a的取值范围是( )
| A、a≤12 | B、a<12 |
| C、a≥12 | D、a>12 |
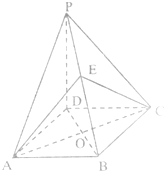 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.