题目内容
已知一个空间几何体的三视图如图所示，且这个空间几何体的所有顶点都在一个球面上，则这个球的体积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体为正三棱柱，其外接球的圆心为上、下底面三角形的中心连线的中点，结合图形与三视图的数据可求AE与OE的长，利用勾股定理可得外接球的半径R，代入球的体积公式计算．
解答：
解：由三视图知几何体为正三棱柱，且三棱柱的底面三角形的边长与侧棱长都为2，如图：
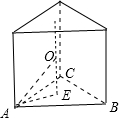
∴其外接球的圆心为上、下底面三角形的中心连线的中点O，
OE=1，AE=
×2×
=
，
∴外接球的半径R=
=
=
，
∴外接球的体积V=
π×(
)3=
π．
故选：B．
∴其外接球的圆心为上、下底面三角形的中心连线的中点O，
OE=1，AE=
| 2 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
∴外接球的半径R=
| OE2+AE2 |
1+
|
| ||
| 3 |
∴外接球的体积V=
| 4 |
| 3 |
| ||
| 3 |
28
| ||
| 27 |
故选：B．
点评：本题考查了由三视图求几何体的外接球的体积，考查了球的体积公式，熟练掌握几何体的结构特征是解答此类问题的关键．
练习册系列答案
相关题目
圆（x-1）2+y2=3的圆心坐标和半径分别是（ ）
| A、（-1，0），3 | ||
| B、（1，0），3 | ||
C、(-1，0)，
| ||
D、(1，0)，
|
已知实数x、y满足条件
，那么x+3y的最大值是（ ）
|
| A、1 | B、3 | C、6 | D、8 |
已知函数f（x）=
，若?a，b，c∈R，f（a），f（b），f（c）为某一个三角形的边长，则实数m的取值范围是（ ）
| ex+m |
| ex+1 |
A、[
| ||
| B、[0，1] | ||
| C、[1，2] | ||
D、[
|
设函数f（x）=
，则f（log23）=（ ）
|
|
| A、13 | B、19 | C、37 | D、49 |
已知向量
=（1，2），
=（2，1），则（
•
）（
-2
）等于（ ）
| m |
| n |
| m |
| n |
| m |
| n |
| A、（-12，0） | B、4 |
| C、（-3，0） | D、-12 |