Question

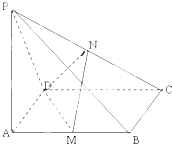如图，PA⊥平面ABCD，四边形ABCD是矩形，PA=AD，M，N分别是AB，PC的中点．
（1）求证：MN∥平面PAD；
（2）求证：平面MND⊥平面PCD．

Answer 1

考点：平面与平面垂直的判定,直线与平面平行的判定

专题：证明题,空间位置关系与距离

分析：（1）要证明MN∥平面PAD，可以想着找一个MN所在平面和平面PAD平行，取CD中点E，连接ME，NE，则容易证明ME∥平面PAD，NE∥平面PAD，所以平面MNE∥平面PAD，这样就能得到MN∥平面PAD；
（2）只要在平面MNE内找一直线和平面PCD垂直即可，通过观察MN像是所找直线，容易证明MN⊥CD，连接PM，CM，能得到PM=CM，所以MN⊥PC，这样这条直线就找到了，也就能证出平面MND⊥平面PCD了．

解答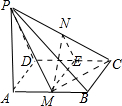： 证明：（1）取CD中点E，连接ME，NE，
则：ME∥AD，NE∥PD，AD?平面PAD，PD?平面PAD；
∴ME∥平面PAD，NE∥平面PAD，NE∩ME=E；
∴平面MNE∥平面PAD，MN?平面MNE；
∴MN∥平面PAD．
（2）∵PA⊥平面ABCD，AB?平面ABCD；
∴PA⊥AB，即AB⊥PA；
又AB⊥AD，PA∩AD=A；
∴AB⊥平面PAD，CD∥AB；
∴CD⊥平面PAD，
∵MN∥平面PAD，CD⊥平面PAD；
∴CD⊥MN，即MN⊥CD，连接PM，CM；
∵AM=BM，PA=CB，∠PAM=∠CBM；
∴△PAM≌△CBM，∴PM=CM，N是PC中点；
∴MN⊥PC，PD∩CD=C，PD，CD?平面PCD；
∴MN⊥平面PCD，MN?平面MNE；
∴平面MND⊥平面PCD．

点评：本题考查线面平行的判定定理，面面平行的判定定理，面面平行的性质，线面垂直的性质，线面垂直的判定定理，面面垂直的判定定理．