题目内容
15.已知数列{an}满足a1=1,an+1=$\frac{a_n}{{2{a_n}+1}}$(n∈N*),bn=$\frac{a_n}{2n+1}$,则数列{bn}的前n项和Sn=$\frac{n}{2n+1}$.分析 先根据数列的递推公式求出数列{an}的通项公式,即可得到数列{bn}的通项公式,裂项求和即可.
解答 解:∵数列{an}满足a1=1,an+1=$\frac{a_n}{{2{a_n}+1}}$(n∈N*),
∴$\frac{1}{{a}_{n+1}}$=$\frac{2{a}_{n}+1}{{a}_{n}}$=2+$\frac{1}{{a}_{n}}$,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=2,
∵$\frac{1}{{a}_{1}}$=1,
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项,以2为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=1+2(n-1)=2n-1,
∴bn=$\frac{a_n}{2n+1}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴数列{bn}的前n项和Sn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$,
故答案为:$\frac{n}{2n+1}$.
点评 本题考查了裂项求和和数列的递推公式,考查了学生的运算能力,属于中档题

练习册系列答案
相关题目
3.设复数z=a+bi(a,b∈R,b>0),且$\overline z={z^2}$,则z的虚部为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{2}$ |
10.近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设30多个分支机构,需要国内公司外派大量70后、80后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从70后和80后的员工中随机调查了100位,得到数据如表:
(Ⅰ)根据调查的数据,是否有90%以上的把握认为“是否愿意被外派与年龄有关”,并说明理由;
(Ⅱ)该公司举行参观驻海外分支机构的交流体验活动,拟安排4名参与调查的70后员工参加.70后员工中有愿意被外派的3人和不愿意被外派的3人报名参加,现采用随机抽样方法从报名的员工中选4人,求选到愿意被外派人数不少于不愿意被外派人数的概率.
参考数据:
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 愿意被外派 | 不愿意被外派 | 合计 | |
| 70后 | 20 | 20 | 40 |
| 80后 | 40 | 20 | 60 |
| 合计 | 60 | 40 | 100 |
(Ⅱ)该公司举行参观驻海外分支机构的交流体验活动,拟安排4名参与调查的70后员工参加.70后员工中有愿意被外派的3人和不愿意被外派的3人报名参加,现采用随机抽样方法从报名的员工中选4人,求选到愿意被外派人数不少于不愿意被外派人数的概率.
参考数据:
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
7.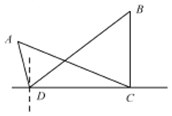 如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )
如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )
 如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )
如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )| A. | $20\sqrt{6}$海里 | B. | $40\sqrt{6}$海里 | C. | $20(1+\sqrt{3})$海里 | D. | 40海里 |
4.在平面直角坐标系中,角α的顶点与原点O重合,始边与x轴的非负半轴重合,点P(-2t,t)(t≠0)是角α终边上的一点,则$tan(α+\frac{π}{4})$的值为( )
| A. | $3-2\sqrt{2}$ | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
5.圆x2+y2-2y=0与曲线y=|x|-1的公共点个数为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 0 |