题目内容
已知数列{an}满足:a1=1,an+1-an=2,n∈N*,数列{an}的前n项和为Sn
(1)求数列{an}的通项公式及前n项和Sn公式;
(2)求数列{
}的前n项和Tn.
(1)求数列{an}的通项公式及前n项和Sn公式;
(2)求数列{
| 1 |
| an•an+1 |
考点:数列的求和,等差数列的前n项和
专题:等差数列与等比数列
分析:(1)直接由等差数列的通项公式和前n项和公式得答案;
(2)把(1)中求得的通项公式代入
,整理后利用裂项相消法求数列{
}的前n项和Tn.
(2)把(1)中求得的通项公式代入
| 1 |
| an•an+1 |
| 1 |
| an•an+1 |
解答:
解:(1)由a1=1,an+1-an=2,n∈N*,得
an=1+2(n-1)=2n-1,
Sn=n+
=n2;
(2)
=
=
(
-
),
则Tn=
[(1-
)+(
-
)+(
-
)+…+(
-
)]
=
(1-
)=
.
an=1+2(n-1)=2n-1,
Sn=n+
| 2n(n-1) |
| 2 |
(2)
| 1 |
| an•an+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
则Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题考查了等差数列的通项公式和前n项和公式,考查了裂项相消法求数列的和,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知幂函数f(x)=(m2-3m+3)•xm+1为偶函数,则m=( )
| A、1 | B、2 | C、1或2 | D、3 |
函数f(x)=
的定义域为M,g(x)=
的定义域为N,则M∩N=( )
| 1 | ||
|
| x+2 |
| A、[-2,+∞) |
| B、[-2,2) |
| C、(-2,2) |
| D、(-∞,2) |
函数f(x)=(x2-2x-3)(x2-2x-5)的值域是( )
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、[24,+∞) |
| D、(24,+∞) |
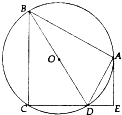 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.