题目内容
7.若x∈(1,+∞),则y=2x+$\frac{1}{x-1}$的最小值是2$\sqrt{2}$+2.分析 变形利用基本不等式的性质即可得出.
解答 解:∵x∈(1,+∞),则y=2(x-1)+$\frac{1}{x-1}$+2≥2$\sqrt{2(x-1)•\frac{1}{x-1}}$+2=2$\sqrt{2}$+2,当且仅当x=1+$\frac{\sqrt{2}}{2}$时取等号.
∴y=2x+$\frac{1}{x-1}$的最小值是2$\sqrt{2}$+2.
故答案为:2$\sqrt{2}$+2.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
18.已知函数f(x)的定义域为[0,2],则函数f(x-3)的定义域为( )
| A. | [-3,-1] | B. | [0,2] | C. | [2,5] | D. | [3,5] |
2.不等式x2-2x+m>0在R上恒成立的充分不必要条件是( )
| A. | m>2 | B. | 0<m<1 | C. | m>0 | D. | m>1 |
19.天气预报显示,在今后的三天中,每一天下雨的概率为40%,现用随机模拟的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0-9之间整数值的随机数,并制定用1,2,3,4,5表示下雨,用5,6,7,8,9,0表示不下雨,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这三天中恰有两天下雨的概率近似为( )
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这三天中恰有两天下雨的概率近似为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
16.已知球O的半径为R,体积为V,则“R>$\sqrt{10}$”是“V>36π”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
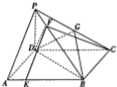 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.