题目内容
4．已知点B（-2，0）、C（2，0），且△ABC的周长等于14，求顶点A的轨迹方程．分析 根据三角形的周长和定点，得到点A到两个定点的距离之和等于定值，得到点A的轨迹是椭圆，椭圆的焦点在y轴上，写出椭圆的方程，去掉不合题意的点．
解答 解：∵△ABC的周长为14，顶点B（-2，0）、C（2，0），
∴BC=4，AB+AC=14-4=10，
由于10＞4，所以点A在以点B（-2，0）、C（2，0）为焦点，长轴长为10的椭圆上，其中a=5，c=2，则b2=a2-c2=52-22=21，
所以点A的轨迹方程为$\frac{x^2}{25}+\frac{y^2}{21}=1$（x≠0）．．
点评 本题考查椭圆的定义，注意椭圆的定义中要检验两个线段的大小，看能不能构成椭圆，本题是一个易错题，容易忽略掉不合题意的点．
练习册系列答案
相关题目
14．函数f（x）=ax3+bx2+cx-34（a，b，c∈R）的导函数为f′（x），若不等式f′（x）≤0的解集为{x|-2≤x≤3}，且f（x）的极小值等于-196，则a的值是（ ）
| A． | -$\frac{81}{22}$ | B． | $\frac{1}{3}$ | C． | 5 | D． | ．4 |
12．若$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$均为单位向量，且$\overrightarrow{a}$•$\overrightarrow{b}$=0，（$\overrightarrow{a}$-$\overrightarrow{c}$）•（$\overrightarrow{b}$-$\overrightarrow{c}$）≤0，则|$\overrightarrow{a}$+$\overrightarrow{b}$-2$\overrightarrow{c}$|的最大值为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{2}$-1 | D． | 2-$\sqrt{2}$ |
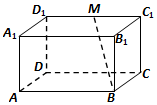如图，在长方体ABCD-A1B1C1D1中，AB=2AD=4，A A1=2$\sqrt{2}$，M是C1D1的中点．