题目内容
4.已知函数$f(x)={log_2}({x^2}+2)$,$\overrightarrow a=(m,1)$,$\overrightarrow b=(\frac{1}{2},\frac{m}{2})$,且m>0,若$f(\overrightarrow a•\overrightarrow b)≥f(|\overrightarrow a-\overrightarrow b|)$,试求m的取值范围.分析 进行数量积的运算,先求出$\overrightarrow{a}•\overrightarrow{b}=m$,$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{\frac{5{m}^{2}}{4}-2m+\frac{5}{4}}$,并且容易判断函数f(x)为偶函数,且单调递增在(0,+∞)上,从而根据$f(\overrightarrow{a}•\overrightarrow{b})≥f(|\overrightarrow{a}-\overrightarrow{b}|)$便可得到不等式$m≥\sqrt{\frac{5}{4}{m}^{2}-2m+\frac{5}{4}}$,这样解该不等式便可得出m的取值范围.
解答 解:∵$\overrightarrow a=(m,1),\overrightarrow b=(\frac{1}{2},\frac{m}{2})$,m>0;
∴$\overrightarrow{a}•\overrightarrow{b}=\frac{m}{2}+\frac{m}{2}=m$,$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{(m-\frac{1}{2})^{2}+(1-\frac{m}{2})^{2}}$=$\sqrt{\frac{5{m}^{2}}{4}-2m+\frac{5}{4}}$;
由$f(x)={log_2}({x^2}+2)$知f(x)为偶函数且在(0,+∞)上单调递增;
∵$f(\overrightarrow a•\overrightarrow b)≥f(|\overrightarrow a-\overrightarrow b|)$;
∴$\overrightarrow a•\overrightarrow b≥|\overrightarrow a-\overrightarrow b|$;
∴$m≥\sqrt{\frac{5}{4}{m^2}-2m+\frac{5}{4}}$且m>0;
∴解得$4-\sqrt{11}≤m≤4+\sqrt{11}$;
∴m的取值范围为$[4-\sqrt{11},4+\sqrt{11}]$.
点评 考查数量积的坐标运算,向量坐标的减法运算,以及偶函数和增函数的定义及判断,无理不等式的解法.

| A. | 最小值4 | B. | 最大值4 | C. | 最小值2 | D. | 最大值2 |
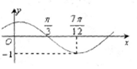 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | -$\frac{81}{22}$ | B. | $\frac{1}{3}$ | C. | 5 | D. | .4 |